On tight contact structures with negative maximal twisting number on
... We can see S as the universal cover of the space of Legendrian curves isotopic to a regular fibre (vertical Legendrian curves from now on). However we would prefer to see the twisting number as a function on the space of vertical Legendrian curves, not on its universal cover. This is the case when t ...
... We can see S as the universal cover of the space of Legendrian curves isotopic to a regular fibre (vertical Legendrian curves from now on). However we would prefer to see the twisting number as a function on the space of vertical Legendrian curves, not on its universal cover. This is the case when t ...
fractal geometry : an introduction
... Geometry, the dimensions fail to coincide; therefore, these sets are called dimensionally discordant. In the early 20th century Karl Menger, L E J Brouwer, Pavel Urysohn and Henri Lebesgue introduced the idea of topological dimension. We denote it by DT. While working in Euclidean space En, both DT ...
... Geometry, the dimensions fail to coincide; therefore, these sets are called dimensionally discordant. In the early 20th century Karl Menger, L E J Brouwer, Pavel Urysohn and Henri Lebesgue introduced the idea of topological dimension. We denote it by DT. While working in Euclidean space En, both DT ...
TopoCheck - Sinergise
... A loop back or self-intersecting polygon is when: 1. The boundary of the polygon crosses itself. This error is sometimes described as a ‘Butterfly’ or ‘Figure of Eight’ polygon, or 2. The line recrosses a vertex in a different direction. These two events are illustrated in the diagrams to the left ...
... A loop back or self-intersecting polygon is when: 1. The boundary of the polygon crosses itself. This error is sometimes described as a ‘Butterfly’ or ‘Figure of Eight’ polygon, or 2. The line recrosses a vertex in a different direction. These two events are illustrated in the diagrams to the left ...
Lectures – Math 128 – Geometry – Spring 2002
... one can be deformed into the other, without making any tears. For (closed, orientable) surfaces, topology essentially boils down to how many holes you have. Definition The geometry of the surface consists of those properties that do change when the surface is deformed. Curvature, distances, angles, ...
... one can be deformed into the other, without making any tears. For (closed, orientable) surfaces, topology essentially boils down to how many holes you have. Definition The geometry of the surface consists of those properties that do change when the surface is deformed. Curvature, distances, angles, ...
3 Main Branches of Modern Mathematics
... Given a set V and a transformation group G on the elements in V. Then V is called a space, its elements is called points, and the subspaces of V is called graphs. And then the study of graphs about the invariants in the group G is called the geometry of V corresponding to G. ...
... Given a set V and a transformation group G on the elements in V. Then V is called a space, its elements is called points, and the subspaces of V is called graphs. And then the study of graphs about the invariants in the group G is called the geometry of V corresponding to G. ...
Department of Mathematics
... 1) Whenever feasible questions may be divided into two parts. Part (a) will follow the traditional pattern, while part (b) will be devoted to true/false type questions. 2) If the last recommendation is followed uniformly for all questions in the paper, the following note should precede the question ...
... 1) Whenever feasible questions may be divided into two parts. Part (a) will follow the traditional pattern, while part (b) will be devoted to true/false type questions. 2) If the last recommendation is followed uniformly for all questions in the paper, the following note should precede the question ...
Read the history below and answer the questions that follow
... one of the three greatest mathematicians of all time, invented non-Euclidian geometry prior to the independent work of Janos Bolyai (1802–1860) and Nikolai Lobachevsky (1792-1856). NonEuclidian geometry generally refers to any geometry not based on the postulates of Euclid, including geometries for ...
... one of the three greatest mathematicians of all time, invented non-Euclidian geometry prior to the independent work of Janos Bolyai (1802–1860) and Nikolai Lobachevsky (1792-1856). NonEuclidian geometry generally refers to any geometry not based on the postulates of Euclid, including geometries for ...
Modern geometry 2012.8.27 - 9. 5 Introduction to Geometry Ancient
... Carl Friedrich Gauss had actually studied the problem before that, but he did not publish any of his results. The resulting geometries were later developed by Lobachevsky, Riemann and Poincaré into hyperbolic geometry and spherical geometry . The independence of the parallel postulate from Euclid's ...
... Carl Friedrich Gauss had actually studied the problem before that, but he did not publish any of his results. The resulting geometries were later developed by Lobachevsky, Riemann and Poincaré into hyperbolic geometry and spherical geometry . The independence of the parallel postulate from Euclid's ...
On Euclidean and Non-Euclidean Geometry by Hukum Singh DESM
... book consisted 13 volumes. The first six volumes consisted study of geometry, seven to ten consisted number theory and last three consisted three dimensional solid geometry. The Euclid axioms are [1], [3] (a)There lie infinite number of points on a line (b) Infinite number of lines passes through a ...
... book consisted 13 volumes. The first six volumes consisted study of geometry, seven to ten consisted number theory and last three consisted three dimensional solid geometry. The Euclid axioms are [1], [3] (a)There lie infinite number of points on a line (b) Infinite number of lines passes through a ...
N-Symmetry Direction Fields on Surfaces of Arbitrary Genus
... of turning number and index to characterize the singularities of a direction field (see Sections 2.5 and 2.6); —We provide an accessible proof of an analog of the Poincaré-Hopf theorem, implying that the indices of the singularities of a N-symmetry direction field defined on a manifold surface S su ...
... of turning number and index to characterize the singularities of a direction field (see Sections 2.5 and 2.6); —We provide an accessible proof of an analog of the Poincaré-Hopf theorem, implying that the indices of the singularities of a N-symmetry direction field defined on a manifold surface S su ...
The Closed Limit Point Compactness
... point ;when he generalized Weierstrass's Theorem to topological spaces. We now know this property as the Bolzano-Weierstrass property, or the limit point compactness ...
... point ;when he generalized Weierstrass's Theorem to topological spaces. We now know this property as the Bolzano-Weierstrass property, or the limit point compactness ...
Use visualization, spatial reasoning, and geometric modeling to
... solve problems such as those involving surface area and volume; continued ...
... solve problems such as those involving surface area and volume; continued ...
The Cantor Set and the Cantor Function
... Yes, in some sense, a whole lot more. But in some other sense, just some dust - which in some ways is scattered, in some other ways it is bound together. We will describe different ways to ”measure” the dust left. This will take us through several mathematical disciplines: set theory, measure theory ...
... Yes, in some sense, a whole lot more. But in some other sense, just some dust - which in some ways is scattered, in some other ways it is bound together. We will describe different ways to ”measure” the dust left. This will take us through several mathematical disciplines: set theory, measure theory ...
Random geometric complexes in the thermodynamic regime
... topological one, and has been well studied in this setting, with [30] being the standard text in the area. There are various ‘regimes’ in which it is natural to study these questions, depending on the radius r. If r is small, then the balls in (1.1) will only rarely overlap, and so the topology of b ...
... topological one, and has been well studied in this setting, with [30] being the standard text in the area. There are various ‘regimes’ in which it is natural to study these questions, depending on the radius r. If r is small, then the balls in (1.1) will only rarely overlap, and so the topology of b ...
Teacher Talk-Standards behind Reasoning
... relationships within, an axiomatic system. • (B)recognize the historical development of geometric systems and know mathematics is developed for a variety of purposes; and • (C)compare and contrast the structures and implications of Euclidean and non-Euclidean geometries. ...
... relationships within, an axiomatic system. • (B)recognize the historical development of geometric systems and know mathematics is developed for a variety of purposes; and • (C)compare and contrast the structures and implications of Euclidean and non-Euclidean geometries. ...
(pdf)
... Now is the appropriate time to talk about Haar measure. We will not go into much detail, but it is a very useful tool. In fact, we will use the properties of Haar measure to prove the Product Formula in a later subsection. Definition 6.1. A Haar measure µ on a locally compact topological group is a ...
... Now is the appropriate time to talk about Haar measure. We will not go into much detail, but it is a very useful tool. In fact, we will use the properties of Haar measure to prove the Product Formula in a later subsection. Definition 6.1. A Haar measure µ on a locally compact topological group is a ...
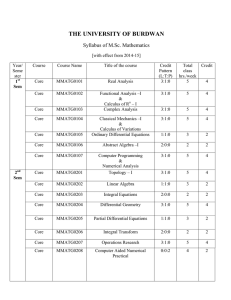
THE UNIVERSITY OF BURDWAN Syllabus of M.Sc. Mathematics
... duration leading to Semester-I, Semester-II, Semester-III and Semester-IV examination in Mathematics at the end of each semester. Syllabus for P.G. courses in Mathematics is hereby framed according to the following schemes and structures. Scheme of course will be Choice based Credit System as per un ...
... duration leading to Semester-I, Semester-II, Semester-III and Semester-IV examination in Mathematics at the end of each semester. Syllabus for P.G. courses in Mathematics is hereby framed according to the following schemes and structures. Scheme of course will be Choice based Credit System as per un ...
BASIC DEFINITIONS IN CATEGORY THEORY MATH 250B 1
... It is easy to see that imF is a subcategory of D. Moreover, imF is a full subcategory if and only if F is full. 5. Isomorphisms and Equivalences of Categories Let C be a category. An isomoprhism f : A → B in C is just an invertible morphism. I.e f is an isomoprhism if there exists g : B → A such tha ...
... It is easy to see that imF is a subcategory of D. Moreover, imF is a full subcategory if and only if F is full. 5. Isomorphisms and Equivalences of Categories Let C be a category. An isomoprhism f : A → B in C is just an invertible morphism. I.e f is an isomoprhism if there exists g : B → A such tha ...
Introduction
... spaces. .G; X / structures have several variants and they have been developed and adapted to various settings by Haefliger, Kuiper, Benzécri, Thurston, Goldman and others to cover new structures, including foliations and singular spaces. The most spectacular advancement in this domain is certainly ...
... spaces. .G; X / structures have several variants and they have been developed and adapted to various settings by Haefliger, Kuiper, Benzécri, Thurston, Goldman and others to cover new structures, including foliations and singular spaces. The most spectacular advancement in this domain is certainly ...
THE UNIFORMIZATION THEOREM AND UNIVERSAL COVERS
... complex plane, the open unit disk, and the Riemann sphere are simply-connected, we will show how to contract any loop to a single point. Take a loop on the complex plane described by a map f and choose an arbitrary point x0 on the loop. We want to show that the loop can be contracted to the point x0 ...
... complex plane, the open unit disk, and the Riemann sphere are simply-connected, we will show how to contract any loop to a single point. Take a loop on the complex plane described by a map f and choose an arbitrary point x0 on the loop. We want to show that the loop can be contracted to the point x0 ...
BPS states of curves in Calabi–Yau 3–folds
... a surface S ⊂ X (see [12], [13], [14]). The nature of the D–brane moduli space in the case where there are non-reduced curves in the family M is not well c → M over a point corresponding to a non-reduced understood. The fiber of M curve may involve higher rank bundles on the reduction of the curve. ...
... a surface S ⊂ X (see [12], [13], [14]). The nature of the D–brane moduli space in the case where there are non-reduced curves in the family M is not well c → M over a point corresponding to a non-reduced understood. The fiber of M curve may involve higher rank bundles on the reduction of the curve. ...
161_syllabus
... Circle Geometry Cartesian Coordinate System, Vector Geometry Angles in Coordinate Geometry, The Complex Plane Birkhos Axiomatic System for Analytic Geometry Review Midterm # 1 Euclidean Constructions Constructibility Background and History of Non-Euclidean Geometry Models of Hyperbolic Geometry Basi ...
... Circle Geometry Cartesian Coordinate System, Vector Geometry Angles in Coordinate Geometry, The Complex Plane Birkhos Axiomatic System for Analytic Geometry Review Midterm # 1 Euclidean Constructions Constructibility Background and History of Non-Euclidean Geometry Models of Hyperbolic Geometry Basi ...
Topology

In mathematics, topology (from the Greek τόπος, place, and λόγος, study), is the study of topological spaces. It is an area of mathematics concerned with the properties of space that are preserved under continuous deformations, such as stretching and bending, but not tearing or gluing. Important topological properties include connectedness and compactness.Topology developed as a field of study out of geometry and set theory, through analysis of such concepts as space, dimension, and transformation. Such ideas go back to Gottfried Leibniz, who in the 17th century envisioned the geometria situs (Greek-Latin for ""geometry of place"") and analysis situs (Greek-Latin for ""picking apart of place""). Leonhard Euler's Seven Bridges of Königsberg Problem and Polyhedron Formula are arguably the field's first theorems. The term topology was introduced by Johann Benedict Listing in the 19th century, although it was not until the first decades of the 20th century that the idea of a topological space was developed. By the middle of the 20th century, topology had become a major branch of mathematics.Topology has many subfields:General topology establishes the foundational aspects of topology and investigates properties of topological spaces and investigates concepts inherent to topological spaces. It includes point-set topology, which is the foundational topology used in all other branches (including topics like compactness and connectedness).Algebraic topology tries to measure degrees of connectivity using algebraic constructs such as homology and homotopy groups.Differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.Geometric topology primarily studies manifolds and their embeddings (placements) in other manifolds. A particularly active area is low dimensional topology, which studies manifolds of four or fewer dimensions. This includes knot theory, the study of mathematical knots.See also: topology glossary for definitions of some of the terms used in topology, and topological space for a more technical treatment of the subject.