Polyhedra and Geodesic Structures
... for human error – and hence this is an “expensive” operation. Drawing an initial line for a construction, however, introduces practically no error – unless your “straightedge” is crooked! Of course, one is free to modify the point system as one sees fit. One might, for example, in order to encourage ...
... for human error – and hence this is an “expensive” operation. Drawing an initial line for a construction, however, introduces practically no error – unless your “straightedge” is crooked! Of course, one is free to modify the point system as one sees fit. One might, for example, in order to encourage ...
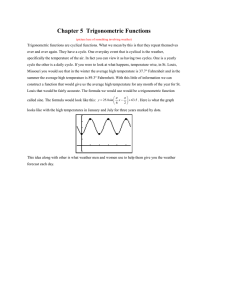
Chapter 5 Trigonometric Functions
... In the first example θ, read “theta”, is the name of the angle between the two rays. In the second example α, read “alpha”, is the name of the angle between its two rays. The point where the two rays start is called the vertex. In trigonometry we will further define angles such that they can have po ...
... In the first example θ, read “theta”, is the name of the angle between the two rays. In the second example α, read “alpha”, is the name of the angle between its two rays. The point where the two rays start is called the vertex. In trigonometry we will further define angles such that they can have po ...
Pants decompositions of random surfaces
... vertices are joined by an edge if the corresponding pants share a boundary. (This trivalent graph may have multiple edges or loops.) We call this graph the topological type of the pants decomposition. We say that two pants decompositions are topologically equivalent if their topological types are is ...
... vertices are joined by an edge if the corresponding pants share a boundary. (This trivalent graph may have multiple edges or loops.) We call this graph the topological type of the pants decomposition. We say that two pants decompositions are topologically equivalent if their topological types are is ...
![[edit] Star polyhedra](http://s1.studyres.com/store/data/000129689_1-21c3cefe8dffc208c8fed163027e6a92-300x300.png)
[edit] Star polyhedra
... pasting six cubes to the sides of one, all seven of the same size; it has 30 square faces (counting disconnected faces in the same plane as separate). This can be extended in one, two, or three directions: we can consider the union of arbitrarily many copies of these structures, obtained by translat ...
... pasting six cubes to the sides of one, all seven of the same size; it has 30 square faces (counting disconnected faces in the same plane as separate). This can be extended in one, two, or three directions: we can consider the union of arbitrarily many copies of these structures, obtained by translat ...
On The Flat-Foldability Of A Crease Pattern
... Remark 7. Notice that Definition 6 is too strict for our aim. For example, in the case of a crease pattern with only two vertices, it is enough to require that at least one of the two conditions of Definition 6 holds in order to ensure that local flat-folding maps which agree can be glued together t ...
... Remark 7. Notice that Definition 6 is too strict for our aim. For example, in the case of a crease pattern with only two vertices, it is enough to require that at least one of the two conditions of Definition 6 holds in order to ensure that local flat-folding maps which agree can be glued together t ...
Task on Parallelograms
... For example, if one wishes to name the quadrilateral to the right, and he/she starts with vertex A and proceeds around the figure in a clockwise direction, then an appropriate name would be quadrilateral ABCD. (Make sure you understand the above paragraph.) ...
... For example, if one wishes to name the quadrilateral to the right, and he/she starts with vertex A and proceeds around the figure in a clockwise direction, then an appropriate name would be quadrilateral ABCD. (Make sure you understand the above paragraph.) ...
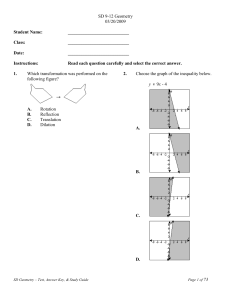
Shortlisted Problems with Solutions
... piiq At any moment, he may double the whole family of imons in his lab by creating a copy I 1 of each imon I. During this procedure, the two copies I 1 and J 1 become entangled if and only if the original imons I and J are entangled, and each copy I 1 becomes entangled with its original imon I; no o ...
... piiq At any moment, he may double the whole family of imons in his lab by creating a copy I 1 of each imon I. During this procedure, the two copies I 1 and J 1 become entangled if and only if the original imons I and J are entangled, and each copy I 1 becomes entangled with its original imon I; no o ...
![arXiv:1007.3607v1 [cs.CG] 21 Jul 2010 On k](http://s1.studyres.com/store/data/014301021_1-0b834295d3acb0403d454bb0d0019afe-300x300.png)
arXiv:1007.3607v1 [cs.CG] 21 Jul 2010 On k
... The notion of convexity is central in geometry. As such, it has been generalized in many ways and for different reasons. In this paper we consider a simple and intuitive generalization of convexity, which to the best of our knowledge has not been worked on. It leads to an appealing class of polygons ...
... The notion of convexity is central in geometry. As such, it has been generalized in many ways and for different reasons. In this paper we consider a simple and intuitive generalization of convexity, which to the best of our knowledge has not been worked on. It leads to an appealing class of polygons ...
The Min-Max Voronoi Diagram of Polygons and Applications in VLSI
... convex hulls. The latter was also shown in [1] for disjoint convex shapes and arbitrary convex distances. Using a divide and conquer algorithm for computing envelopes in three dimensions, [4] concluded that the cluster Voronoi diagram can be constructed in O(n2 α(n)) time. In [1] the problem for dis ...
... convex hulls. The latter was also shown in [1] for disjoint convex shapes and arbitrary convex distances. Using a divide and conquer algorithm for computing envelopes in three dimensions, [4] concluded that the cluster Voronoi diagram can be constructed in O(n2 α(n)) time. In [1] the problem for dis ...
Jeremy L. Martin`s Lecture Notes on Algebraic Combinatorics
... • Πn is a lattice. The meet of two partitions is their “coarsest common refinement”: x, y belong to the same block of S ∧ T if and only if they belong to the same block of S and to the same block of T . The join is the transitive closure of the union of the equivalence relations corresponding to S a ...
... • Πn is a lattice. The meet of two partitions is their “coarsest common refinement”: x, y belong to the same block of S ∧ T if and only if they belong to the same block of S and to the same block of T . The join is the transitive closure of the union of the equivalence relations corresponding to S a ...
Mod 2 Cohomology of Combinatorial Grassmannians
... hyperplane V and the “distinguished side” is ∅.) By considering a form as the inner product with a vector, we arrive at yet another way of viewing an realizable oriented matroid: Take a finite collection E = {v1 , . . . , vn } of vectors in a finite dimensional real inner product space V , then the ...
... hyperplane V and the “distinguished side” is ∅.) By considering a form as the inner product with a vector, we arrive at yet another way of viewing an realizable oriented matroid: Take a finite collection E = {v1 , . . . , vn } of vectors in a finite dimensional real inner product space V , then the ...
10 - Haiku Learning
... is true or false. If the statement is true, provide a diagram to support it. If the statement is false, explain why. 18. A pair of obtuse angles can also be vertical angles. 19. A pair of straight angles can also be adjacent angles. ...
... is true or false. If the statement is true, provide a diagram to support it. If the statement is false, explain why. 18. A pair of obtuse angles can also be vertical angles. 19. A pair of straight angles can also be adjacent angles. ...
PDF version - Rice University
... Every polyhedron, regular and non-regular, convex and concave, has a dihedral angle at every edge. A dihedral angle (also called the face angle) is the internal angle at which two adjacent faces meet. An angle of zero degrees means the face normal vectors are anti-parallel and the faces overlap each ...
... Every polyhedron, regular and non-regular, convex and concave, has a dihedral angle at every edge. A dihedral angle (also called the face angle) is the internal angle at which two adjacent faces meet. An angle of zero degrees means the face normal vectors are anti-parallel and the faces overlap each ...
MLI final Project-Ping
... Every polyhedron, regular and non-regular, convex and concave, has a dihedral angle at every edge. A dihedral angle (also called the face angle) is the internal angle at which two adjacent faces meet. An angle of zero degrees means the face normal vectors are anti-parallel and the faces overlap each ...
... Every polyhedron, regular and non-regular, convex and concave, has a dihedral angle at every edge. A dihedral angle (also called the face angle) is the internal angle at which two adjacent faces meet. An angle of zero degrees means the face normal vectors are anti-parallel and the faces overlap each ...
The Most Charming Subject in Geometry
... Every polyhedron, regular and non-regular, convex and concave, has a dihedral angle at every edge. A dihedral angle (also called the face angle) is the internal angle at which two adjacent faces meet. An angle of zero degrees means the face normal vectors are anti-parallel and the faces overlap each ...
... Every polyhedron, regular and non-regular, convex and concave, has a dihedral angle at every edge. A dihedral angle (also called the face angle) is the internal angle at which two adjacent faces meet. An angle of zero degrees means the face normal vectors are anti-parallel and the faces overlap each ...
