Derivation of the Quantum Hamilton Equations of Motion and
... As part of this series of papers [1–10] developing the Einstein Cartan Evans (ECE) unified field theory, the fermion equation of motion of relativistic quantum mechanics has been derived in the three preceding papers (UFT 172 to UFT 174 on www.aias.us). In Section 2, the methods used to develop the ...
... As part of this series of papers [1–10] developing the Einstein Cartan Evans (ECE) unified field theory, the fermion equation of motion of relativistic quantum mechanics has been derived in the three preceding papers (UFT 172 to UFT 174 on www.aias.us). In Section 2, the methods used to develop the ...
Why the Logical Disjunction in Quantum Logic is Not
... is true. This means that the state p of the quantum entity is such that whenever a undergoes a ‘yes-no’ test α, the outcome ‘yes’ can be predicted with certainty (probability equal to 1). As we know, such a ‘yes-no’ test in quantum mechanics is represented by the self adjoint operator, the spectral ...
... is true. This means that the state p of the quantum entity is such that whenever a undergoes a ‘yes-no’ test α, the outcome ‘yes’ can be predicted with certainty (probability equal to 1). As we know, such a ‘yes-no’ test in quantum mechanics is represented by the self adjoint operator, the spectral ...
Chapter 12 Quantum gases
... In classical statistical mechanics, we dealt with an ideal gas which was a good approximation for a real gas in the highly diluted limit. An important difference between classical and quantum mechanical many-body systems lies in the distinguishable character of their constituent particles. The inher ...
... In classical statistical mechanics, we dealt with an ideal gas which was a good approximation for a real gas in the highly diluted limit. An important difference between classical and quantum mechanical many-body systems lies in the distinguishable character of their constituent particles. The inher ...
Comparison of 3D classical and quantum mechanical He scattering
... quantum mechanics? Since the interaction is generally strong, EhrenfestÕs theorem invalidates the picture of the trajectories. If we adhere the purely stochastic (``Heidelberg approach'') discussion of quantum chaos; the dwell time of atoms near the surface has to be determined as a function of appr ...
... quantum mechanics? Since the interaction is generally strong, EhrenfestÕs theorem invalidates the picture of the trajectories. If we adhere the purely stochastic (``Heidelberg approach'') discussion of quantum chaos; the dwell time of atoms near the surface has to be determined as a function of appr ...
Complexity of one-dimensional spin chains
... states must violate a transition rule after at most O(m2) transitions, so have a (polynomially small) positive energy. • States which have the right structure and n qubits: The transition rules and boundary conditions select only a correct history state as the ground state of the Hamiltonian. ...
... states must violate a transition rule after at most O(m2) transitions, so have a (polynomially small) positive energy. • States which have the right structure and n qubits: The transition rules and boundary conditions select only a correct history state as the ground state of the Hamiltonian. ...
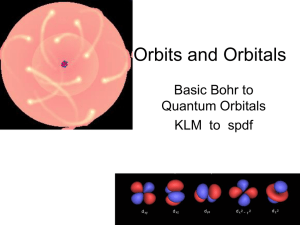
Orbits and Orbitals
... • Now we know that KLM is “really” the “Principle Quantum Number” 1,2,3 for the energy levels • spdf – refers to the shape of the “orbital” – ...
... • Now we know that KLM is “really” the “Principle Quantum Number” 1,2,3 for the energy levels • spdf – refers to the shape of the “orbital” – ...
L14special - Particle Physics and Particle Astrophysics
... emit photons, losing energy constantly and eventually spiralling into the nucleus. This doesn’t happen!! ...
... emit photons, losing energy constantly and eventually spiralling into the nucleus. This doesn’t happen!! ...
Seminar Report
... definition, is not the actual time taken to multiply a particular pairs of number but the fact that the time does not increase too sharply when we apply the same method to ever larger numbers. The same standard text-book method of multiplication requires little extra work when we switch from two 3 - ...
... definition, is not the actual time taken to multiply a particular pairs of number but the fact that the time does not increase too sharply when we apply the same method to ever larger numbers. The same standard text-book method of multiplication requires little extra work when we switch from two 3 - ...
Scattering model for quantum random walk on the hypercube
... search in a database with the topology of the hypercube faster that it can be done classically [2]. It is an oracle based algorithm, which is optimal in its speed. Another successful application of quantum random walks has been demonstrated by Childs, et al. citechilds2003 who have also constructed ...
... search in a database with the topology of the hypercube faster that it can be done classically [2]. It is an oracle based algorithm, which is optimal in its speed. Another successful application of quantum random walks has been demonstrated by Childs, et al. citechilds2003 who have also constructed ...
A Functional Architecture for Scalable Quantum Computing
... qubit gates and 102 ns for the SWAP class gates in the 40qubit example from Figure 2, with an average T1 = 10µs, and two-qubit fidelity of 99.69% would result in a TQF of 3921. From an algorithmic perspective, TQF gives a rough estimates of the size of the quantum circuit (circuit width times circui ...
... qubit gates and 102 ns for the SWAP class gates in the 40qubit example from Figure 2, with an average T1 = 10µs, and two-qubit fidelity of 99.69% would result in a TQF of 3921. From an algorithmic perspective, TQF gives a rough estimates of the size of the quantum circuit (circuit width times circui ...
Reverse Causality and the Transactional Interpretation
... The simple answer is “No!”. It is the formalism of quantum mechanics that makes all of the testable predictions. As long as an interpretation like the TI is consistent with the formalism, it will make the same predictions as any other valid interpretation, and no experimental tests are possible. ...
... The simple answer is “No!”. It is the formalism of quantum mechanics that makes all of the testable predictions. As long as an interpretation like the TI is consistent with the formalism, it will make the same predictions as any other valid interpretation, and no experimental tests are possible. ...