Geometry - Grade 4 Common Core Math
... same endpoint. This endpoint is called the vertex. The two rays that form the angle are called sides. ...
... same endpoint. This endpoint is called the vertex. The two rays that form the angle are called sides. ...
Discovering Geometry Day 3
... perpendicular lines – lines that intersect to form four 90° angles. skew lines – lines that do not lie in the same plane. On pages 49–50, define the terms in bold. right angle – an angle that measures 90°. acute angle – an angle that measures between 0° and 90°. obtuse angle – an angle that measur ...
... perpendicular lines – lines that intersect to form four 90° angles. skew lines – lines that do not lie in the same plane. On pages 49–50, define the terms in bold. right angle – an angle that measures 90°. acute angle – an angle that measures between 0° and 90°. obtuse angle – an angle that measur ...
Geometry Claims Unit 1: Geometric Structure Geometric structure
... Similarity should be studied outside of the classroom and not inside of the classroom. It is easier/more aesthetically pleasing to create quilts with similar/congruent triangles. In a equilateral/right isosceles triangle, it is easier to calculate the length of a missing side using the propert ...
... Similarity should be studied outside of the classroom and not inside of the classroom. It is easier/more aesthetically pleasing to create quilts with similar/congruent triangles. In a equilateral/right isosceles triangle, it is easier to calculate the length of a missing side using the propert ...
VOCABULARY: Parallel lines, parallel planes, skew lines
... 2.9.11.G Solve problems using analytic geometry. 2.8.11.J Demonstrate the connection between algebraic equations and inequalities and the geometry of relations in the coordinate plane. 2.8.11.L Write the equation of a line when given the graph of the line, two points on the line, or the slope of the ...
... 2.9.11.G Solve problems using analytic geometry. 2.8.11.J Demonstrate the connection between algebraic equations and inequalities and the geometry of relations in the coordinate plane. 2.8.11.L Write the equation of a line when given the graph of the line, two points on the line, or the slope of the ...
3-3 Notes
... 3-3 Proving Lines Parallel Example 1A: Using the Converse of the Corresponding Angles Postulate Given the information to show that ℓ || m. ...
... 3-3 Proving Lines Parallel Example 1A: Using the Converse of the Corresponding Angles Postulate Given the information to show that ℓ || m. ...
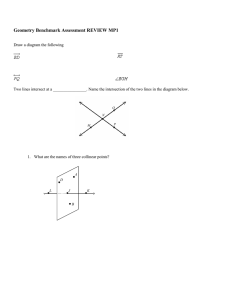
Geometry Benchmark Assessment REVIEW MP1 Answer Section
... ____ 33. Each unit on the map represents 5 miles. What is the actual distance from Oceanfront to Seaside? y ...
... ____ 33. Each unit on the map represents 5 miles. What is the actual distance from Oceanfront to Seaside? y ...
... Sometimes (when the segments lie on parallel lines) If two lines are cut by a transversal, the rays bisecting a pair of alternate interior angles are parallel. Sometimes – if the two lines cut by the transversal are parallel The opposite angles of a parallelogram are supplementary Sometimes (when it ...
Chapter 3 - Woodland Hills School District
... Name angles formed by a pair of lines and a transversal Use the properties of parallel lines to determine congruent angles Use algebra to find angle measures Find slopes of lines and use slope to identify parallel and perpendicular lines Write an equation of a line given information about ...
... Name angles formed by a pair of lines and a transversal Use the properties of parallel lines to determine congruent angles Use algebra to find angle measures Find slopes of lines and use slope to identify parallel and perpendicular lines Write an equation of a line given information about ...
3-3 Proving Lines Parallel
... 6. Vert.∠s Thm. 7. Substitution 8. Conv. of Same-Side Interior ∠s Post. ...
... 6. Vert.∠s Thm. 7. Substitution 8. Conv. of Same-Side Interior ∠s Post. ...
1. The following figure is a box in which the top and bottom are
... Yes, for example all three can be 60 degrees. c. Can a triangle have two right angles? Why or why not? No, because the remaining angle would have measure zero. d. If a triangle has one acute angle, is the triangle necessarily acute? Why or why not? No, one of the other angles may be obtuse, making i ...
... Yes, for example all three can be 60 degrees. c. Can a triangle have two right angles? Why or why not? No, because the remaining angle would have measure zero. d. If a triangle has one acute angle, is the triangle necessarily acute? Why or why not? No, one of the other angles may be obtuse, making i ...
4_Math_G1 - mcsfourthgrade
... Anson County ~ Bladen County ~ Columbus County ~ Cumberland County ~ Ft. Bragg ~ Harnett County ~ Hoke County Lee County ~ Montgomery County ~ Moore County ~ Richmond County ~ Robeson County ~ Scotland County ~ Whiteville City ...
... Anson County ~ Bladen County ~ Columbus County ~ Cumberland County ~ Ft. Bragg ~ Harnett County ~ Hoke County Lee County ~ Montgomery County ~ Moore County ~ Richmond County ~ Robeson County ~ Scotland County ~ Whiteville City ...
Geometry Level 1 Curriculum
... and/or paragraph arguments always with the idea of a clear, logical argument with mathematical justification as a priority. A major focus in this unit is on quadrilaterals. Properties of quadrilaterals are introduced through various discovery activities in order to build a quadrilateral tree and to ...
... and/or paragraph arguments always with the idea of a clear, logical argument with mathematical justification as a priority. A major focus in this unit is on quadrilaterals. Properties of quadrilaterals are introduced through various discovery activities in order to build a quadrilateral tree and to ...
Perspective (graphical)

Perspective (from Latin: perspicere to see through) in the graphic arts is an approximate representation, on a flat surface (such as paper), of an image as it is seen by the eye. The two most characteristic features of perspective are that objects are smaller as their distance from the observer increases; and that they are subject to foreshortening, meaning that an object's dimensions along the line of sight are shorter than its dimensions across the line of sight.Italian Renaissance painters including Paolo Uccello, Piero della Francesca and Luca Pacoima studied linear perspective, wrote treatises on it, and incorporated it into their artworks, thus contributing to the mathematics of art.