Proving Triangles and Quadrilaterals are Special
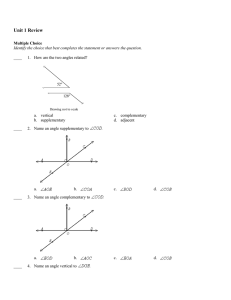
... Consider ΔTAP'. Since two sides are equal, it is isosceles, so ∠RTA = ∠RP'A. RP is also rotated 180˚ around a point not on the line, so image is parallel to pre-image. That is, PR || P'A. Using transversal TP', we see that ∠RP'A = ∠TRP. Thus ∠RTA = ∠RP'A= ∠TRP. Because two angles in ΔTRB are eq ...
... Consider ΔTAP'. Since two sides are equal, it is isosceles, so ∠RTA = ∠RP'A. RP is also rotated 180˚ around a point not on the line, so image is parallel to pre-image. That is, PR || P'A. Using transversal TP', we see that ∠RP'A = ∠TRP. Thus ∠RTA = ∠RP'A= ∠TRP. Because two angles in ΔTRB are eq ...
isosceles trapezoid
... An isosceles trapezoid is a trapezoid whose legs are congruent and that has two congruent angles such that their common side is a base of the trapezoid. Thus, in an isosceles trapezoid, any two angles whose common side is a base of the trapezoid are congruent. In Euclidean geometry, the convention i ...
... An isosceles trapezoid is a trapezoid whose legs are congruent and that has two congruent angles such that their common side is a base of the trapezoid. Thus, in an isosceles trapezoid, any two angles whose common side is a base of the trapezoid are congruent. In Euclidean geometry, the convention i ...
review 1
... 70. Write a paragraph proof of this theorem: In a plane, if two lines are perpendicular to the same line, then they are parallel to each other. ...
... 70. Write a paragraph proof of this theorem: In a plane, if two lines are perpendicular to the same line, then they are parallel to each other. ...
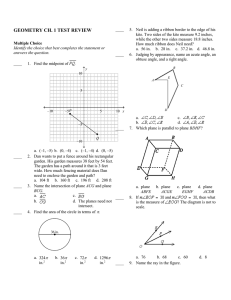
GEOMETRY CH
... ____ 50. A high school soccer team is going to Columbus to see a professional soccer game. A coordinate grid is superimposed on a highway map of Ohio. The high school is at point (3, 4) and the stadium in Columbus is at point (7, 1). The map shows a highway rest stop halfway between the cities. What ...
... ____ 50. A high school soccer team is going to Columbus to see a professional soccer game. A coordinate grid is superimposed on a highway map of Ohio. The high school is at point (3, 4) and the stadium in Columbus is at point (7, 1). The map shows a highway rest stop halfway between the cities. What ...
module
... If a line can pass through three or more points, then these points are said to be collinear. For example the points A, B and C in the Fig. 10.9 are collinear points. If a line can not be drawn passing through all three points (or more points), then they are said to be non-collinear. For example poin ...
... If a line can pass through three or more points, then these points are said to be collinear. For example the points A, B and C in the Fig. 10.9 are collinear points. If a line can not be drawn passing through all three points (or more points), then they are said to be non-collinear. For example poin ...
Perspective (graphical)

Perspective (from Latin: perspicere to see through) in the graphic arts is an approximate representation, on a flat surface (such as paper), of an image as it is seen by the eye. The two most characteristic features of perspective are that objects are smaller as their distance from the observer increases; and that they are subject to foreshortening, meaning that an object's dimensions along the line of sight are shorter than its dimensions across the line of sight.Italian Renaissance painters including Paolo Uccello, Piero della Francesca and Luca Pacoima studied linear perspective, wrote treatises on it, and incorporated it into their artworks, thus contributing to the mathematics of art.