Euclidean Geometry and History of Non
... 3. Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center. 4. All right angles are congruent. 5. Through a point not on a given straight line, one and only one line can be drawn that never meets the given line. The fifth postulate is called the ...
... 3. Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center. 4. All right angles are congruent. 5. Through a point not on a given straight line, one and only one line can be drawn that never meets the given line. The fifth postulate is called the ...
Chapter 13 Geometry
... Failing this, the Man of Steel would like to fly between his current position and the target. He can see through objects, but not fly through them. His desired path flies straight to the goal, until it bumps into an object. At this point, he flies along the boundary of the circle until he returns to ...
... Failing this, the Man of Steel would like to fly between his current position and the target. He can see through objects, but not fly through them. His desired path flies straight to the goal, until it bumps into an object. At this point, he flies along the boundary of the circle until he returns to ...
MADISON PUBLIC SCHOOL DISTRICT Geometry Madison Public
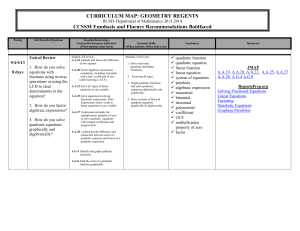
... G.GPE.7: Use coordinates to compute perimeters of polygons and areas of triangles and rectangles, e.g., using the distance formula.★ Translate between the geometric description and the equation for a conic section. G.GPE.2: Derive the equation of a parabola given a focus and directrix. Unit 5: Circl ...
... G.GPE.7: Use coordinates to compute perimeters of polygons and areas of triangles and rectangles, e.g., using the distance formula.★ Translate between the geometric description and the equation for a conic section. G.GPE.2: Derive the equation of a parabola given a focus and directrix. Unit 5: Circl ...
G4_unit 6_16
... Standard 4.MD.5 Recognize angles as geometric shapes that are formed wherever two rays share a common endpoint, and understand concepts of angle measurement: 4.MD.5.a An angle is measured with reference to a circle with its center at the common endpoint of the rays, by considering the fraction of th ...
... Standard 4.MD.5 Recognize angles as geometric shapes that are formed wherever two rays share a common endpoint, and understand concepts of angle measurement: 4.MD.5.a An angle is measured with reference to a circle with its center at the common endpoint of the rays, by considering the fraction of th ...
Conjectures Chapter 2
... opposite side into two segments whose lengths are in the same ratio as the lengths of the two sides forming the angle. [C-96 p. 609] Proportional Areas Conjecture: If corresponding side lengths of two similar polygons or the radii of two circles compare in the ratio ...
... opposite side into two segments whose lengths are in the same ratio as the lengths of the two sides forming the angle. [C-96 p. 609] Proportional Areas Conjecture: If corresponding side lengths of two similar polygons or the radii of two circles compare in the ratio ...
Non-Euclidean Geometry - Department of Mathematics | Illinois
... ◦ 3: Given a point and a distance a circle can be drawn with the point as center and the distance as radius ◦ 4: All right angles are equal ◦ 5: Given a point p and a line l, there is exactly one line through p that is parallel to l ...
... ◦ 3: Given a point and a distance a circle can be drawn with the point as center and the distance as radius ◦ 4: All right angles are equal ◦ 5: Given a point p and a line l, there is exactly one line through p that is parallel to l ...
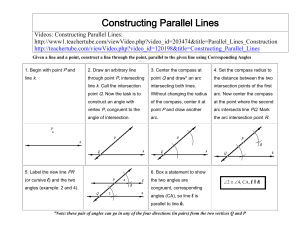
Exploring Parallel Lines and Related Angles
... 11. Prove: If two parallel lines are cut by a transversal, then alternate interior angles are congruent. Given: l || m Prove: ∠3 ≅ ∠6 12. Prove: If two parallel lines are cut by a transversal, then the pairs of same side interior angles are supplementary. Given: l || m Prove: ∠3 and ∠5 are ...
... 11. Prove: If two parallel lines are cut by a transversal, then alternate interior angles are congruent. Given: l || m Prove: ∠3 ≅ ∠6 12. Prove: If two parallel lines are cut by a transversal, then the pairs of same side interior angles are supplementary. Given: l || m Prove: ∠3 and ∠5 are ...
Perspective (graphical)

Perspective (from Latin: perspicere to see through) in the graphic arts is an approximate representation, on a flat surface (such as paper), of an image as it is seen by the eye. The two most characteristic features of perspective are that objects are smaller as their distance from the observer increases; and that they are subject to foreshortening, meaning that an object's dimensions along the line of sight are shorter than its dimensions across the line of sight.Italian Renaissance painters including Paolo Uccello, Piero della Francesca and Luca Pacoima studied linear perspective, wrote treatises on it, and incorporated it into their artworks, thus contributing to the mathematics of art.