Unit 6 Lesson 7 Outline
... Lesson Plan Outline Geometry in Construction Title: Tangent Lines to Circles ...
... Lesson Plan Outline Geometry in Construction Title: Tangent Lines to Circles ...
Point A - nkobersteinkhs
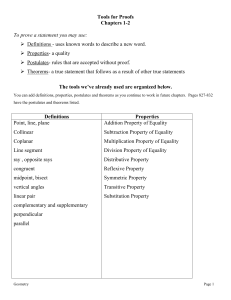
... You can name a line by any two points on the line. Another way to name a line is with a single lowercase letter. ...
... You can name a line by any two points on the line. Another way to name a line is with a single lowercase letter. ...
Solutions - Stony Brook Mathematics
... model, and line, point, or circle to refer to the “usual” Euclidean meanings in R2 . First, let’s check I1: Given two points P = (x1 , y1 ) and Q = (x2 , y2 ), we need to confirm that they determine a unique line. There are two cases: First, suppose that P and Q are collinear with the origin in R2 . ...
... model, and line, point, or circle to refer to the “usual” Euclidean meanings in R2 . First, let’s check I1: Given two points P = (x1 , y1 ) and Q = (x2 , y2 ), we need to confirm that they determine a unique line. There are two cases: First, suppose that P and Q are collinear with the origin in R2 . ...
Final exam key
... (a) Which of these is a theorem in neutral geometry? (A) Given any triangle ∆ABC and any segment DE, there exists a triangle ∆DEF (having DE as one of its sides) that is similar to ∆ABC. (B) If two lines cut by a transversal l have a pair of congruent alternate interior angles with respect to l, the ...
... (a) Which of these is a theorem in neutral geometry? (A) Given any triangle ∆ABC and any segment DE, there exists a triangle ∆DEF (having DE as one of its sides) that is similar to ∆ABC. (B) If two lines cut by a transversal l have a pair of congruent alternate interior angles with respect to l, the ...
10R - donnellymath
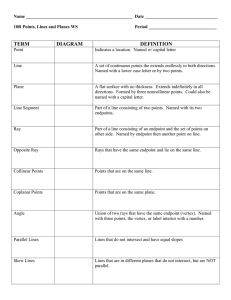
... _____3. Two lines perpendicular to the same plane are coplanar. _____4. Two planes are perpendicular to each other if and only if one plane contains a line perpendicular to the second plane. ...
... _____3. Two lines perpendicular to the same plane are coplanar. _____4. Two planes are perpendicular to each other if and only if one plane contains a line perpendicular to the second plane. ...
Pretest Review Geometry
... A series of points that extends in 2 opposite directions without end Can name a line by any two points on the line with a line above it, or by a single lower case letter. (Please note: In Geometry, it is important to use the correct notations!!) ...
... A series of points that extends in 2 opposite directions without end Can name a line by any two points on the line with a line above it, or by a single lower case letter. (Please note: In Geometry, it is important to use the correct notations!!) ...
Geometry Vocabulary Graphic Organizer
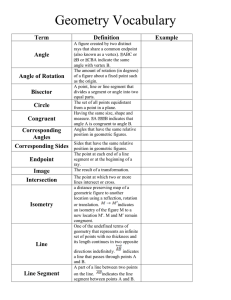
... Sides that have the same relative position in geometric figures. The point at each end of a line segment or at the beginning of a ray. The result of a transformation. The point at which two or more lines intersect or cross. a distance preserving map of a geometric figure to another location using a ...
... Sides that have the same relative position in geometric figures. The point at each end of a line segment or at the beginning of a ray. The result of a transformation. The point at which two or more lines intersect or cross. a distance preserving map of a geometric figure to another location using a ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.