Constructive Geometry and the Parallel Postulate
... we would have to make very drastic assumptions about what it means to be “given” a point or a line. For example, if we were to assume that every point has rational coordinates relative to some lines chosen as the x and y axes, then we could compute whether p lies on L or not; but that would require ...
... we would have to make very drastic assumptions about what it means to be “given” a point or a line. For example, if we were to assume that every point has rational coordinates relative to some lines chosen as the x and y axes, then we could compute whether p lies on L or not; but that would require ...
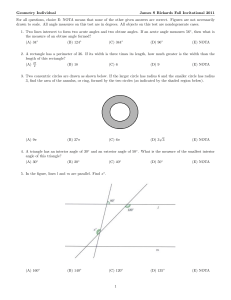
4-7
... A and B are on the edges of a ravine. What is AB? One angle pair is congruent, because they are vertical angles. Two pairs of sides are congruent, because their lengths are equal. Therefore the two triangles are congruent by SAS. By CPCTC, the third side pair is congruent, so AB = 18 mi. Holt McDoug ...
... A and B are on the edges of a ravine. What is AB? One angle pair is congruent, because they are vertical angles. Two pairs of sides are congruent, because their lengths are equal. Therefore the two triangles are congruent by SAS. By CPCTC, the third side pair is congruent, so AB = 18 mi. Holt McDoug ...
Pseudo-integrable billiards and arithmetic dynamics
... is called a saddle-connections. A saddle-connection with coinciding endpoints is called a homoclinic loop. All other billiard trajectories, those that never reach the vertex of an reflex angle, are called regular trajectories. Billiards in domains bounded by several confocal quadrics, without singul ...
... is called a saddle-connections. A saddle-connection with coinciding endpoints is called a homoclinic loop. All other billiard trajectories, those that never reach the vertex of an reflex angle, are called regular trajectories. Billiards in domains bounded by several confocal quadrics, without singul ...
On characterizations of Euclidean spaces
... arbitrarily chosen unit) of the corresponding sector of the unit circle (normalized to 2π). This also defines an angular bisector. ...
... arbitrarily chosen unit) of the corresponding sector of the unit circle (normalized to 2π). This also defines an angular bisector. ...
Postulates - cloudfront.net
... Postulate 20 Side-Angle-Side (SAS) Congruence Postulate: If two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then the two triangles are congruent. Postulate 21 ...
... Postulate 20 Side-Angle-Side (SAS) Congruence Postulate: If two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then the two triangles are congruent. Postulate 21 ...
5.3 Parallel Lines and Congruent Angles
... Goal 1: How to identify angles formed by two lines and a transversal Goal 2: How to use properties of parallel lines ...
... Goal 1: How to identify angles formed by two lines and a transversal Goal 2: How to use properties of parallel lines ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.