3. The parallel axiom Axiom 8 (Parallel Axiom). Given a line k, and a
... We remark that the point of the axiom is not the existence of the parallel, but the uniqueness. We will see below that existence actually follows from what we already know. It is sometimes convenient to think of a line as being parallel to itself, so we make the following formal definition. Two line ...
... We remark that the point of the axiom is not the existence of the parallel, but the uniqueness. We will see below that existence actually follows from what we already know. It is sometimes convenient to think of a line as being parallel to itself, so we make the following formal definition. Two line ...
NC–PIMS Geometry 6-12 - MELT-Institute
... were a regular hexagon? Is it possible to find shapes other than a circle that have the same "width" in every direction? Figures with this property are called curves of constant width, and their study leads to some interesting mathematics and to some alternative manhole cover shapes. ...
... were a regular hexagon? Is it possible to find shapes other than a circle that have the same "width" in every direction? Figures with this property are called curves of constant width, and their study leads to some interesting mathematics and to some alternative manhole cover shapes. ...
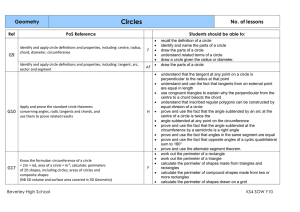
Act. 4.3: Angles Formed by Chords, Tangents and Secants
... A chord is a line segment with both endpoints on the circle A tangent is a line that touches the circle at one point N (the “point of tangency”) D R ...
... A chord is a line segment with both endpoints on the circle A tangent is a line that touches the circle at one point N (the “point of tangency”) D R ...
Geometry Regents Exam 0610 www.jmap.org 1 In the diagram
... 7 A transversal intersects two lines. Which condition would always make the two lines parallel? 1) Vertical angles are congruent. 2) Alternate interior angles are congruent. 3) Corresponding angles are supplementary. 4) Same-side interior angles are complementary. ...
... 7 A transversal intersects two lines. Which condition would always make the two lines parallel? 1) Vertical angles are congruent. 2) Alternate interior angles are congruent. 3) Corresponding angles are supplementary. 4) Same-side interior angles are complementary. ...
Geometry Honors - School District of Marshfield
... A. Apply the no-choice and AAs Theorems Third Quarter 5 cont. (3 Weeks) B. Use formulas involving polygons C. Prove triangles are similar D. Write proportions for similar triangles ...
... A. Apply the no-choice and AAs Theorems Third Quarter 5 cont. (3 Weeks) B. Use formulas involving polygons C. Prove triangles are similar D. Write proportions for similar triangles ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.