5 The hyperbolic plane
... If X is any reasonable topological space, one can form its universal covering space X̃ (see [3]) which is simply connected and has • a projection p : X̃ → X • every point x ∈ X has a neighbourhood V such that p−1 (V ) consists of a disjoint union of open sets each of which is homeomorphic to V by p ...
... If X is any reasonable topological space, one can form its universal covering space X̃ (see [3]) which is simply connected and has • a projection p : X̃ → X • every point x ∈ X has a neighbourhood V such that p−1 (V ) consists of a disjoint union of open sets each of which is homeomorphic to V by p ...
Geometry 1: Intro to Geometry Introduction to Geometry
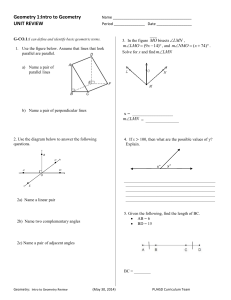
... angles. 15. Draw a diagram that fits the following criteria: Draw two lines and a transversal such that 1 and 2 are corresponding angles, 2 and 3 are vertical angles, and 3 and 4 are corresponding angles. What type of angle pair is 1 and 4? ...
... angles. 15. Draw a diagram that fits the following criteria: Draw two lines and a transversal such that 1 and 2 are corresponding angles, 2 and 3 are vertical angles, and 3 and 4 are corresponding angles. What type of angle pair is 1 and 4? ...
A Quick Introduction to Non-Euclidean Geometry
... 2. A line that meets one of two parallels also meets the other. 3. There exists a triangle whose angle-sum is two right angles. 4. Parallel lines are equidistant from one another. 5. Similar triangles exist which are not congruent. 6. Any two parallel lines have a common perpendicular. 7. Playfair’s ...
... 2. A line that meets one of two parallels also meets the other. 3. There exists a triangle whose angle-sum is two right angles. 4. Parallel lines are equidistant from one another. 5. Similar triangles exist which are not congruent. 6. Any two parallel lines have a common perpendicular. 7. Playfair’s ...
parallel lines - Cloudfront.net
... Line BC are both infinite lines in the same plane. They intersect at point B and , therefore, they are NOT parallel Hyperbolic lines. Hyperbolic line DE and Hyperbolic Line BA are also both infinite lines in the same plane, and since they do not intersect, DE is parallel to BA. Likewise, Hyperbolic ...
... Line BC are both infinite lines in the same plane. They intersect at point B and , therefore, they are NOT parallel Hyperbolic lines. Hyperbolic line DE and Hyperbolic Line BA are also both infinite lines in the same plane, and since they do not intersect, DE is parallel to BA. Likewise, Hyperbolic ...
The Poincaré disc model
... Models for non-Euclidean Geometry • Lobachevsky gave axioms for non-Euclidean geometry and derived theorems, but did not provide a model which has non-Euclidean behavior. • The first (partial) model was constructed by Eugenio Beltrami (1935-1900) in 1868. • Felix Klein (1849-1925) gave an improved • ...
... Models for non-Euclidean Geometry • Lobachevsky gave axioms for non-Euclidean geometry and derived theorems, but did not provide a model which has non-Euclidean behavior. • The first (partial) model was constructed by Eugenio Beltrami (1935-1900) in 1868. • Felix Klein (1849-1925) gave an improved • ...
MATH 161 SAMPLE FINAL EXAM SOLUTIONS 1. Euclidean geometry
... (Note: there are a few different ways to prove this, but in any case to get started you should think of a way to construct a segment satisfying the definition of “height” so that you can use the hypothesis on the heights.) Problem 4 (4 points). Prove that if f is an isometry and f ◦ f is the identit ...
... (Note: there are a few different ways to prove this, but in any case to get started you should think of a way to construct a segment satisfying the definition of “height” so that you can use the hypothesis on the heights.) Problem 4 (4 points). Prove that if f is an isometry and f ◦ f is the identit ...
INTRO Slide Show
... Beginning in the 1960’s, since analytic geometry is used to illustrate the development of concepts in calculus, colleges began referring to their calculus courses as “Calculus and Analytic Geometry.” However, the only real geometry being done involved equations for lines, circles, and conic sections ...
... Beginning in the 1960’s, since analytic geometry is used to illustrate the development of concepts in calculus, colleges began referring to their calculus courses as “Calculus and Analytic Geometry.” However, the only real geometry being done involved equations for lines, circles, and conic sections ...
Hyperbolic Geometry - DigitalCommons@University of Nebraska
... not on a given straight line, one and only one line can be drawn that never meets the given line.), mathematicians were still troubled by it’s complexity, and were convinced that it could be proven as a theorem using the other four axioms. Many tried to find a proof by contradiction. They either ass ...
... not on a given straight line, one and only one line can be drawn that never meets the given line.), mathematicians were still troubled by it’s complexity, and were convinced that it could be proven as a theorem using the other four axioms. Many tried to find a proof by contradiction. They either ass ...
Last year`s exam questions
... MAT402H5F page 5 of 12 (3) For each of the following statements, specify whether it is true or false, and, in one sentence, explain why. (a) In hyperbolic geometry, if 4ABC and 4DEF are equilateral triangles and A ∼ = D, then the triangles are congruent. ...
... MAT402H5F page 5 of 12 (3) For each of the following statements, specify whether it is true or false, and, in one sentence, explain why. (a) In hyperbolic geometry, if 4ABC and 4DEF are equilateral triangles and A ∼ = D, then the triangles are congruent. ...
"Here`s to Looking at Euclid" A Snapshot of Hyperbolic Geometry
... The distance between two parallels with common perpendicular is least when measured along that perpendicular. The distance from a point on either parallel to the other increases as the point recedes from the perpendicular in either direction. ...
... The distance between two parallels with common perpendicular is least when measured along that perpendicular. The distance from a point on either parallel to the other increases as the point recedes from the perpendicular in either direction. ...
Lecture 7
... infinity. Such a vertex is called an ideal vertex. If all the vertices lie on ∂H then we call P an ideal polygon. Notice that the angle at an ideal vertex is zero; this is because all geodesics meet ∂H at right-angles and so the angle between any two such geodesics is zero. (i) ...
... infinity. Such a vertex is called an ideal vertex. If all the vertices lie on ∂H then we call P an ideal polygon. Notice that the angle at an ideal vertex is zero; this is because all geodesics meet ∂H at right-angles and so the angle between any two such geodesics is zero. (i) ...
Non-Euclidean Geometry
... In the Euclidean geometry, make a straight line AB in two parallel lines, circle in a counterclockwise direction with a straight line AB, and then make a circle in a clockwise direction with a straight line AB. From the intersection of the two circles If the vertical CD is perpendicular to the strai ...
... In the Euclidean geometry, make a straight line AB in two parallel lines, circle in a counterclockwise direction with a straight line AB, and then make a circle in a clockwise direction with a straight line AB. From the intersection of the two circles If the vertical CD is perpendicular to the strai ...
WHAT IS HYPERBOLIC GEOMETRY? - School of Mathematics, TIFR
... Gauss started thinking of parallels about 1792. In an 1824 letter to F. A. Taurinus, he wrote: ‘The assumption that the sum of the three angles (of a triangle) is smaller than two right angles leads to a geometry which is quite different from our (Euclidean) geometry, but which is in itself complete ...
... Gauss started thinking of parallels about 1792. In an 1824 letter to F. A. Taurinus, he wrote: ‘The assumption that the sum of the three angles (of a triangle) is smaller than two right angles leads to a geometry which is quite different from our (Euclidean) geometry, but which is in itself complete ...
49. INTRODUCTION TO ANALYTIC GEOMETRY
... Analytic Geometry Analytic geometry, usually called coordinate geometry and earlier referred to as Cartesian geometry or analytical geometry, is the study of geometry using the principles of algebra ...
... Analytic Geometry Analytic geometry, usually called coordinate geometry and earlier referred to as Cartesian geometry or analytical geometry, is the study of geometry using the principles of algebra ...
Triangle reflection groups
... Area(L(α)) = 0 0 sin φdφdθ = 2α. Theorem 2.1. For any spherical triangle T with angles α, β, γ, Area(T ) = (α + β + γ) − π Corollary 2.2. For any spherical triangle T with angles α, β, γ, α +β +γ > π. Proof. Extend the sides of the triangle into three great circles. These great circles divide the sp ...
... Area(L(α)) = 0 0 sin φdφdθ = 2α. Theorem 2.1. For any spherical triangle T with angles α, β, γ, Area(T ) = (α + β + γ) − π Corollary 2.2. For any spherical triangle T with angles α, β, γ, α +β +γ > π. Proof. Extend the sides of the triangle into three great circles. These great circles divide the sp ...
A Brief History of Geometry
... 4. “that all right angles are equal to each other.” 5. “That if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right ...
... 4. “that all right angles are equal to each other.” 5. “That if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right ...
Mathematical Arguments and Triangle Geometry
... Hyperbolic Triangles • Generally the sum of the angles of a hyperbolic triangle is less than 180 • The difference between the calculated sum and 180 is called the defect of the ...
... Hyperbolic Triangles • Generally the sum of the angles of a hyperbolic triangle is less than 180 • The difference between the calculated sum and 180 is called the defect of the ...
Geometry 1:Intro to Geometry UNIT REVIEW
... 10. Draw acute ABC and then construct its bisector. Label all your points. ...
... 10. Draw acute ABC and then construct its bisector. Label all your points. ...
Emina
... the straight line, if produced indefinitely, meet on that side on which are the angles less than two right angles. ...
... the straight line, if produced indefinitely, meet on that side on which are the angles less than two right angles. ...
The PDF of our notes about Kant and Euclidean Geometry
... less than 180 degrees sum interior angles. • Spherical: a triangle in a spherical geometry can have more than 180 degrees sum interior angles. • Remember Kant’s example of a necessary truth of geom ...
... less than 180 degrees sum interior angles. • Spherical: a triangle in a spherical geometry can have more than 180 degrees sum interior angles. • Remember Kant’s example of a necessary truth of geom ...
Non-Euclidean Geometry
... A special thank to the teachers that have this project made possible Mrs Maria Luisa Pozzi Lolli and Mrs ...
... A special thank to the teachers that have this project made possible Mrs Maria Luisa Pozzi Lolli and Mrs ...
I. Fill-in the blanks. II. True or False III. Problem Solving
... Let O be the orthocenter of △ABC. Then ℓ(O, A) is an altitude, so ℓ(O, A) ⊥ ℓ(B, C). Since, ℓ(K, D) is also perpendicular to ℓ(B, C), then ℓ(O, A) is parallel to ℓ(K, D). Let P be the midpoint of OA P . and let H be the center of the nine-point circle. Thus, P is on the nine point circle and HP is ...
... Let O be the orthocenter of △ABC. Then ℓ(O, A) is an altitude, so ℓ(O, A) ⊥ ℓ(B, C). Since, ℓ(K, D) is also perpendicular to ℓ(B, C), then ℓ(O, A) is parallel to ℓ(K, D). Let P be the midpoint of OA P . and let H be the center of the nine-point circle. Thus, P is on the nine point circle and HP is ...
Taxicab Geometry
... Type of geometry generally taught in High School Named after mathematician Euclid, circa 300 BC Created under several assumptions ...
... Type of geometry generally taught in High School Named after mathematician Euclid, circa 300 BC Created under several assumptions ...
Hyperbolic Geometry
... 2. Construct a new unit disk. Create a d-triangle with the tool d-triangle. Construct the perpendicular bisector for each side of the d-triangle. (use midpoint and perpendicular at a point) Does the circumcenter exist? How can you confirm the point is the circumcenter? The supposed circumcenter exis ...
... 2. Construct a new unit disk. Create a d-triangle with the tool d-triangle. Construct the perpendicular bisector for each side of the d-triangle. (use midpoint and perpendicular at a point) Does the circumcenter exist? How can you confirm the point is the circumcenter? The supposed circumcenter exis ...
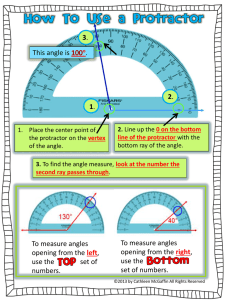
How to Use a Protractor
... To measure angles opening from the right, use the set of numbers. ©2013 by Cathleen McGaffin All Rights Reserved ...
... To measure angles opening from the right, use the set of numbers. ©2013 by Cathleen McGaffin All Rights Reserved ...
Hyperbolic geometry
In mathematics, hyperbolic geometry (also called Bolyai–Lobachevskian geometry or Lobachevskian geometry) is a non-Euclidean geometry. In hyperbolic geometry the parallel postulate of Euclidean geometry is replaced with:For any given line R and point P not on R, in the plane containing both line R and point P there are at least two distinct lines through P that do not intersect R.(compare this with Playfair's axiom the modern version of Euclid's parallel postulate)Hyperbolic plane geometry is also the geometry of saddle surface or pseudospherical surfaces, surfaces with a constant negative Gaussian curvature.A modern use of hyperbolic geometry is in the theory of special relativity, particularly Minkowski spacetime and gyrovector space.When geometers first realised they worked with something else than the standard Euclidean geometry they described their geometry under many different names; Felix Klein finally gave the subject the name hyperbolic geometry. It was for putting it in the now rarely used sequence elliptic geometry (spherical geometry) , parabolic geometry (Euclidean geometry), and hyperbolic geometry.In Russia it is commonly called Lobachevskian geometry after one of its discoverers, the Russian geometer Nikolai Lobachevsky.This page is mainly about the 2 dimensional or plane hyperbolic geometry and the differences and similarities between Euclidean and hyperbolic geometry.Hyperbolic geometry can be extended to three and more dimensions; see hyperbolic space for more on the three and higher dimensional cases.