optimal angle bounds for quadrilateral meshes
... mesh on the disk. In this section we describe the subdomain and how to subdivide it into circular arc triangles, quadrilaterals and pentagons. In the following sections we show how to construct quadrilateral meshes for each subregions that are consistent along shared boundaries. A compact hyperbolic ...
... mesh on the disk. In this section we describe the subdomain and how to subdivide it into circular arc triangles, quadrilaterals and pentagons. In the following sections we show how to construct quadrilateral meshes for each subregions that are consistent along shared boundaries. A compact hyperbolic ...
Polygons
... amount of light they reflect. A pentagon is a type of polygon. Prefixes are used to name different types of polygons. ...
... amount of light they reflect. A pentagon is a type of polygon. Prefixes are used to name different types of polygons. ...
4.1: Congruent Figures Congruent Polygons: Corresponding Angles
... 4.1: Congruent Figures Congruent Polygons: Corresponding Angles: Corresponding Sides: Congruence Statement: Naming Polygons: 1) List the vertices by starting at one and working around (the corners of the figure) 2) If it’s a triangle use a small triangle in front of the vertices, for anything else, ...
... 4.1: Congruent Figures Congruent Polygons: Corresponding Angles: Corresponding Sides: Congruence Statement: Naming Polygons: 1) List the vertices by starting at one and working around (the corners of the figure) 2) If it’s a triangle use a small triangle in front of the vertices, for anything else, ...
Geometry
... Midsegment of a Triangle Definition-a segment that joins the midpoints of two sides of a triangle. The midsegment of a triangle is parallel to the third side. The midsegment of a triangle is one-half the length of the third side. The three midsegments of a triangle divide the triangle into f ...
... Midsegment of a Triangle Definition-a segment that joins the midpoints of two sides of a triangle. The midsegment of a triangle is parallel to the third side. The midsegment of a triangle is one-half the length of the third side. The three midsegments of a triangle divide the triangle into f ...
Geometry - New Paltz Central School District
... 1. How does your knowledge of Euclidean 2-D geometry theorems validate 3-D solids? 2. How is volume derived from area? 3. When and why have these shapes been used in ancient history? Time May-Jun (4 wks) ...
... 1. How does your knowledge of Euclidean 2-D geometry theorems validate 3-D solids? 2. How is volume derived from area? 3. When and why have these shapes been used in ancient history? Time May-Jun (4 wks) ...
Classifying Triangles
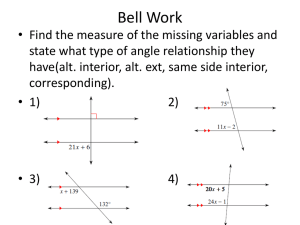
... Classify each triangle by its angle measures as acute, equiangular, right, or obtuse. (Note: Give two classifications for Exercise 7.) ...
... Classify each triangle by its angle measures as acute, equiangular, right, or obtuse. (Note: Give two classifications for Exercise 7.) ...
File
... _____ 1. Triangles that are the same size and shape. _____ 2. Two angles and a nonincluded side of one triangle must be congruent to the same in the other triangle. _____ 3. The three sides of one triangle must be congruent to the three sides of the other triangle. _____ 4. Two sides and the include ...
... _____ 1. Triangles that are the same size and shape. _____ 2. Two angles and a nonincluded side of one triangle must be congruent to the same in the other triangle. _____ 3. The three sides of one triangle must be congruent to the three sides of the other triangle. _____ 4. Two sides and the include ...
No Slide Title
... of a ravine. What is AB? One angle pair is congruent, because they are vertical angles. Two pairs of sides are congruent, because their lengths are equal. Therefore the two triangles are congruent by SAS. By CPCTC, the third side pair is congruent, so AB = 18 mi. Holt Geometry ...
... of a ravine. What is AB? One angle pair is congruent, because they are vertical angles. Two pairs of sides are congruent, because their lengths are equal. Therefore the two triangles are congruent by SAS. By CPCTC, the third side pair is congruent, so AB = 18 mi. Holt Geometry ...
Building Polygons
... and difficult situations. Make notes about when you do not receive a point during a turn. Why did you not need to move any corners ...
... and difficult situations. Make notes about when you do not receive a point during a turn. Why did you not need to move any corners ...
axonometric plane - Design Communication Graphics
... The viewing position may be lowered or raised. The position of the axonometric plane will rotate so that it remains perpendicular to the viewing direction ...
... The viewing position may be lowered or raised. The position of the axonometric plane will rotate so that it remains perpendicular to the viewing direction ...
Tessellation

A tessellation of a flat surface is the tiling of a plane using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellations can be generalized to higher dimensions and a variety of geometries.A periodic tiling has a repeating pattern. Some special kinds include regular tilings with regular polygonal tiles all of the same shape, and semi-regular tilings with regular tiles of more than one shape and with every corner identically arranged. The patterns formed by periodic tilings can be categorized into 17 wallpaper groups. A tiling that lacks a repeating pattern is called ""non-periodic"". An aperiodic tiling uses a small set of tile shapes that cannot form a repeating pattern. In the geometry of higher dimensions, a space-filling or honeycomb is also called a tessellation of space.A real physical tessellation is a tiling made of materials such as cemented ceramic squares or hexagons. Such tilings may be decorative patterns, or may have functions such as providing durable and water-resistant pavement, floor or wall coverings. Historically, tessellations were used in Ancient Rome and in Islamic art such as in the decorative tiling of the Alhambra palace. In the twentieth century, the work of M. C. Escher often made use of tessellations, both in ordinary Euclidean geometry and in hyperbolic geometry, for artistic effect. Tessellations are sometimes employed for decorative effect in quilting. Tessellations form a class of patterns in nature, for example in the arrays of hexagonal cells found in honeycombs.