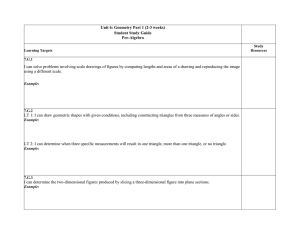
Mathematics - Renton School District
... Solve linear equations in one variable. a. Give examples of linear equations in one variable with one solution, infinitely many solutions, or no solutions. Show which of these possibilities is the case by successively transforming the given equation into simpler forms, until an equivalent equation o ...
... Solve linear equations in one variable. a. Give examples of linear equations in one variable with one solution, infinitely many solutions, or no solutions. Show which of these possibilities is the case by successively transforming the given equation into simpler forms, until an equivalent equation o ...
Warm-Up`s #111-120
... Iris wants to buy two necklaces, one for her sister and one for herself. The necklace for her sister costs $42.00, and the necklace for herself costs $28.00. The sales tax on the purchases is 8%. Find the total cost of Iris’s purchases, including sales tax. If necessary, round your answer to the nea ...
... Iris wants to buy two necklaces, one for her sister and one for herself. The necklace for her sister costs $42.00, and the necklace for herself costs $28.00. The sales tax on the purchases is 8%. Find the total cost of Iris’s purchases, including sales tax. If necessary, round your answer to the nea ...
Vocabulary Chapter 1A
... Measure of an angle- number that corresponds to the size of the angle, usually given in degrees Acute angles- angles with a measure greater than 0° and less than 90° Right Angles- angles with a measure of 90° Obtuse Angles- angles with a measure greater than 90° and less than 180° Perimeter (of a pl ...
... Measure of an angle- number that corresponds to the size of the angle, usually given in degrees Acute angles- angles with a measure greater than 0° and less than 90° Right Angles- angles with a measure of 90° Obtuse Angles- angles with a measure greater than 90° and less than 180° Perimeter (of a pl ...
Course Learning Objectives - Mathematical Sciences
... problems involving right triangles. They extend the definitions of the trigonometric functions beyond right triangles using the unit circle and they measure angles in radians as well as degrees. The draw and analyze graphs of trigonometric functions (including finding period, amplitude, and phase sh ...
... problems involving right triangles. They extend the definitions of the trigonometric functions beyond right triangles using the unit circle and they measure angles in radians as well as degrees. The draw and analyze graphs of trigonometric functions (including finding period, amplitude, and phase sh ...
Semester 1 Final Review B
... tall oak tree across the street. Eager to identify the bird, he stands in the doorway and looks through his binoculars, so that he doesn’t scare the bird away. Brian’s eyes are 5.7 feet off the ground, and he estimates that his angle of sight up to the bird is 55°. How far is Brian from the base of ...
... tall oak tree across the street. Eager to identify the bird, he stands in the doorway and looks through his binoculars, so that he doesn’t scare the bird away. Brian’s eyes are 5.7 feet off the ground, and he estimates that his angle of sight up to the bird is 55°. How far is Brian from the base of ...
Unit Title - RoybalLearningCenterLAUSD
... Solve problems using the distance formula. congruence, points, and planes. Find the midpoint of a line segment. Construct a perpendicular bisector. Add line segments. Add angles. Manipulate formulas for lines without numerical values (using letters). ...
... Solve problems using the distance formula. congruence, points, and planes. Find the midpoint of a line segment. Construct a perpendicular bisector. Add line segments. Add angles. Manipulate formulas for lines without numerical values (using letters). ...
Multilateration
Multilateration (MLAT) is a navigation technique based on the measurement of the difference in distance to two stations at known locations that broadcast signals at known times. Unlike measurements of absolute distance or angle, measuring the difference in distance between two stations results in an infinite number of locations that satisfy the measurement. When these possible locations are plotted, they form a hyperbolic curve. To locate the exact location along that curve, multilateration relies on multiple measurements: a second measurement taken to a different pair of stations will produce a second curve, which intersects with the first. When the two curves are compared, a small number of possible locations are revealed, producing a ""fix"".Multilateration is a common technique in radio navigation systems, where it is known as hyperbolic navigation. These systems are relatively easy to construct as there is no need for a common clock, and the difference in the signal timing can be measured visibly using an oscilloscope. This formed the basis of a number of widely used navigation systems starting in World War II with the British Gee system and several similar systems introduced over the next few decades. The introduction of the microprocessor greatly simplified operation, greatly increasing popularity during the 1980s. The most popular hyperbolic navigation system was LORAN-C, which was used around the world until the system was shut down in 2010. Other systems continue to be used, but the widespread use of satellite navigation systems like GPS have made these systems largely redundant.Multilateration should not be confused with trilateration, which uses distances or absolute measurements of time-of-flight from three or more sites, or with triangulation, which uses the measurement of absolute angles. Both of these systems are also commonly used with radio navigation systems.