SMSG Geometry Summary
... half-plane, we say that they lie on the same side of L; if P lies in one of the half-planes and Q in the other they lie on opposite sides of L. 4. Postulate 10. (The Space Separation Postulate.) The points of space that do not lie in a given plane form two sets such that (1) each of the sets is conv ...
... half-plane, we say that they lie on the same side of L; if P lies in one of the half-planes and Q in the other they lie on opposite sides of L. 4. Postulate 10. (The Space Separation Postulate.) The points of space that do not lie in a given plane form two sets such that (1) each of the sets is conv ...
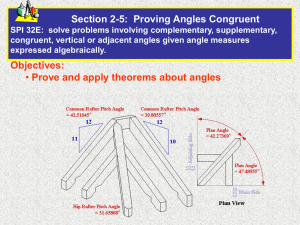
Do Now
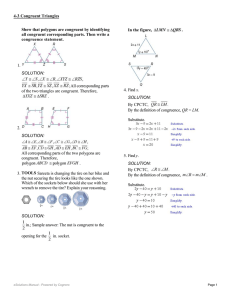
... Step 3: Fold the paper so that the other pair of vertical angles lie over each other. What do you notice about their measures? ...
... Step 3: Fold the paper so that the other pair of vertical angles lie over each other. What do you notice about their measures? ...
We Choose Many Parallels!
... Lemma 7.3 The fourth angle of a Lambert quadrilateral is acute. Proof: If the fourth angle were obtuse, our quadrilateral would have an angle sum greater than 360◦ , which cannot happen. If the angle were a right angle, then a rectangle would exist and all triangles would have to have defect 0. Sinc ...
... Lemma 7.3 The fourth angle of a Lambert quadrilateral is acute. Proof: If the fourth angle were obtuse, our quadrilateral would have an angle sum greater than 360◦ , which cannot happen. If the angle were a right angle, then a rectangle would exist and all triangles would have to have defect 0. Sinc ...