Recall from yesterday the two conjectures that you derived about the
... ***Remember: The Reflexive Property of Congruence was covered in Chapter 2 page 106. An included angle is________________________________________________________. In order for the SAS Conjecture to be valid, the angle chosen MUST be the one included between the two chosen sides! Not just any old ang ...
... ***Remember: The Reflexive Property of Congruence was covered in Chapter 2 page 106. An included angle is________________________________________________________. In order for the SAS Conjecture to be valid, the angle chosen MUST be the one included between the two chosen sides! Not just any old ang ...
MATH 5: ASSIGNMENT 12 Today we are starting a
... intersects both of them by a third line as shown in the figure to the right, then angles labeled by letters a1 , a2 will be equal. Conversely, if these two angles are equal, then the lines must be parallel. ...
... intersects both of them by a third line as shown in the figure to the right, then angles labeled by letters a1 , a2 will be equal. Conversely, if these two angles are equal, then the lines must be parallel. ...
5.5 Triangle Inequalities
... 5. Tell whether a triangle can have the given sides with lengths. Show all three inequalities to find b . ]\A ^'5-- Q >5~- ^ ^ your answer, a. 6, 10, and 15 ^ 1o - f l S > ^ b. 11.9, 5.8,and 5.8 /\ D 6. Aaron, Brandon, and Clara sit in class so that they form the vertices of a triangle. Aaron is 15 ...
... 5. Tell whether a triangle can have the given sides with lengths. Show all three inequalities to find b . ]\A ^'5-- Q >5~- ^ ^ your answer, a. 6, 10, and 15 ^ 1o - f l S > ^ b. 11.9, 5.8,and 5.8 /\ D 6. Aaron, Brandon, and Clara sit in class so that they form the vertices of a triangle. Aaron is 15 ...
2 - Geometry And Measurement
... 3) Two line are described by the equations: y=3x+5 and 5y-25=15x which of the following is true about the equation for these two lines? ...
... 3) Two line are described by the equations: y=3x+5 and 5y-25=15x which of the following is true about the equation for these two lines? ...
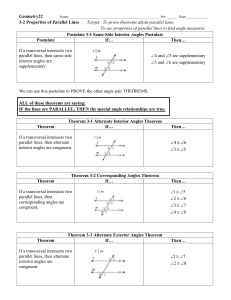
Geometry22 Name: Per: ______ Date: ______ 3
... ALL of these theorems are saying: IF the lines are PARALLEL, THEN the special angle relationships are true. ...
... ALL of these theorems are saying: IF the lines are PARALLEL, THEN the special angle relationships are true. ...
Sacccheri`s proof of the parallel postulate
... Proof. Let line AP fall on AD and P L, such that AP K P L and =P AD is an acute angle. To show that AD will intersect P L. We cut of segments AM1 “ M1 M2 “ M2 M3 , and so on; and draw M1 N1 ∥ M2 N2 ∥ M3 N3 , and so on. Then AN1 ď N1 N2 ď N2 N3 ď N3 N4 ď ... If this process is continued indefinitely, ...
... Proof. Let line AP fall on AD and P L, such that AP K P L and =P AD is an acute angle. To show that AD will intersect P L. We cut of segments AM1 “ M1 M2 “ M2 M3 , and so on; and draw M1 N1 ∥ M2 N2 ∥ M3 N3 , and so on. Then AN1 ď N1 N2 ď N2 N3 ď N3 N4 ď ... If this process is continued indefinitely, ...
Definitions and concepts
... We DEFINE space to be the set of all points. We DEFINE a geometric figure to be a subset of space. (p. 39) ...
... We DEFINE space to be the set of all points. We DEFINE a geometric figure to be a subset of space. (p. 39) ...
2.5 Proving Angles Congruent
... (5x – 20) and (3x + 8) are vertical angles. (5x + 4y) and (5x – 20) are supplementary angles. Find x and y. Draw a picture of the vertical and supplementary angles. ...
... (5x – 20) and (3x + 8) are vertical angles. (5x + 4y) and (5x – 20) are supplementary angles. Find x and y. Draw a picture of the vertical and supplementary angles. ...