Quiz 4 Review (Blank)
... 25. Go to http://mathopenref.com/tocs/constructionstoc.html and learn how to construct the incenter and circumcenter. ...
... 25. Go to http://mathopenref.com/tocs/constructionstoc.html and learn how to construct the incenter and circumcenter. ...
Infinite Geometry - Chapter 9 Test Review
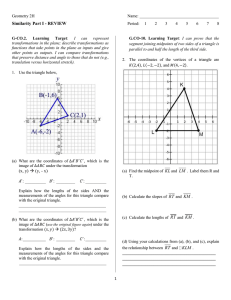
... Find the missing side of each triangle. Round your answers to the nearest tenth if necessary. ...
... Find the missing side of each triangle. Round your answers to the nearest tenth if necessary. ...