3.3 Prove Lines are Parallel
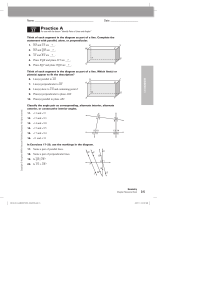
... If two lines are cut by a transversal so that alternate exterior angles are congruent, then the lines are parallel. Converse of Consecutive Interior ...
... If two lines are cut by a transversal so that alternate exterior angles are congruent, then the lines are parallel. Converse of Consecutive Interior ...
Math Circle Beginners Group May 15, 2016 Geometry II
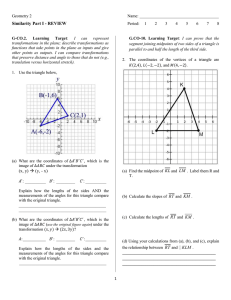
... So, we know that \BAD + \ADC + \DCB + \CBA = 360 . Substituting, we get, (x + 12) + (x + 12) + 156 + 156 = 360. Solving, we get, x = 12 . Finally, \ADE = 156 ...
... So, we know that \BAD + \ADC + \DCB + \CBA = 360 . Substituting, we get, (x + 12) + (x + 12) + 156 + 156 = 360. Solving, we get, x = 12 . Finally, \ADE = 156 ...