STAARCategory 3
... C. The length of the radius of a circle is twice the length of the diameter. D. The length of the radius of a circle is ...
... C. The length of the radius of a circle is twice the length of the diameter. D. The length of the radius of a circle is ...
Lesson
... 1. Make a conjecture about the next item in the sequence: 5, 20, 80, 320. 2. Write the contrapositive for this statement: If you live in Boston, then you live in Massachusetts. 3. Use the Law of Detachment or the Law of Syllogism to determine whether a valid conclusion can be reached from the follow ...
... 1. Make a conjecture about the next item in the sequence: 5, 20, 80, 320. 2. Write the contrapositive for this statement: If you live in Boston, then you live in Massachusetts. 3. Use the Law of Detachment or the Law of Syllogism to determine whether a valid conclusion can be reached from the follow ...
Indiana Academic Standards for Mathematics
... the graph of f is concave upward on the interval if f' is increasing on the interval and concave downward on the interval if f' is decreasing on the interval measures the probability of an event given that another event has occurred a statement that can be written in the if-then form a three- dimens ...
... the graph of f is concave upward on the interval if f' is increasing on the interval and concave downward on the interval if f' is decreasing on the interval measures the probability of an event given that another event has occurred a statement that can be written in the if-then form a three- dimens ...
CCGPS Culminating Task
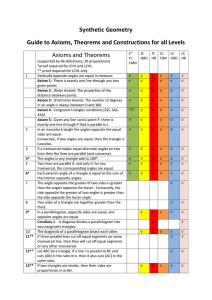
... congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints. MCC9-12.G.CO.10 Prove theorems about triangles. Theor ...
... congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints. MCC9-12.G.CO.10 Prove theorems about triangles. Theor ...
School Calendar - Knott County Schools
... I can apply properties of 45-45Ratios 90 and 30-60-90 triangles to G.SRT.8 determine lengths of sides of triangles G.SRT.11 I can find the sine, cosine, and tangent ratios of acute angles G.SRT.10 given the side lengths of right G.SRT.9 triangles I can use trigonometric ratios to find the sides or a ...
... I can apply properties of 45-45Ratios 90 and 30-60-90 triangles to G.SRT.8 determine lengths of sides of triangles G.SRT.11 I can find the sine, cosine, and tangent ratios of acute angles G.SRT.10 given the side lengths of right G.SRT.9 triangles I can use trigonometric ratios to find the sides or a ...
Slide 1
... to the measures of the angles in each pair. Then find the unknown angle measures. 1. m1 = 120°, m2 = (60x)° Alt. Ext. s Thm.; m2 = 120° 2. m2 = (75x – 30)°, m3 = (30x + 60)° Corr. s Post.; m2 = 120°, m3 = 120° 3. m3 = (50x + 20)°, m4= (100x – 80)° Alt. Int. s Thm.; m3 = 120°, m4 =120° ...
... to the measures of the angles in each pair. Then find the unknown angle measures. 1. m1 = 120°, m2 = (60x)° Alt. Ext. s Thm.; m2 = 120° 2. m2 = (75x – 30)°, m3 = (30x + 60)° Corr. s Post.; m2 = 120°, m3 = 120° 3. m3 = (50x + 20)°, m4= (100x – 80)° Alt. Int. s Thm.; m3 = 120°, m4 =120° ...