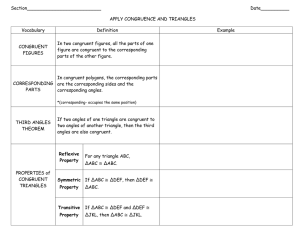
CCR High School Math II
... congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints. Implementation may be extended to include concurrence of perpendicular bisectors M.2HS.42 and angle bisectors as preparation for M.2HS.C.3. Instructional Note: Encourage m ...
... congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints. Implementation may be extended to include concurrence of perpendicular bisectors M.2HS.42 and angle bisectors as preparation for M.2HS.C.3. Instructional Note: Encourage m ...
The Word Geometry
... geometry called Principles of Geometry. In 1840 he published Geometrical researches on the theory of parallels in German In 1855 Gauss recognized the merits of this theory, and recommended him to the Gottingen Society, where he became a member. ...
... geometry called Principles of Geometry. In 1840 he published Geometrical researches on the theory of parallels in German In 1855 Gauss recognized the merits of this theory, and recommended him to the Gottingen Society, where he became a member. ...
Geometry Session 6: Classifying Triangles Activity Sheet
... We saw in Session 5 that symmetry can be used for classifying designs. We will try this for triangles. The activity sheet for sorting triangles has several triangles to classify, but instead of ...
... We saw in Session 5 that symmetry can be used for classifying designs. We will try this for triangles. The activity sheet for sorting triangles has several triangles to classify, but instead of ...