Geometry_How much do I know - Homepage | Talk Maths Talk
... Some shapes are composite shapes, which need to be split up into their basic elements (rectangles/triangles). There is often more than one way to do this. In the example above, we have a rectangle and a triangle. We can either use the triangle area formula directly to find the area of the shaded tri ...
... Some shapes are composite shapes, which need to be split up into their basic elements (rectangles/triangles). There is often more than one way to do this. In the example above, we have a rectangle and a triangle. We can either use the triangle area formula directly to find the area of the shaded tri ...
IM7 - Unit 7 Geometric Figures.docx
... (7.G.2) Draw (freehand, with ruler and protractor, and with technology) geometric shapes with given conditions. Focus on constructing triangles from three measures of angles or sides, noticing when the conditions determine a unique triangle, more than one triangle, or no triangle. (7.G.3) Describe t ...
... (7.G.2) Draw (freehand, with ruler and protractor, and with technology) geometric shapes with given conditions. Focus on constructing triangles from three measures of angles or sides, noticing when the conditions determine a unique triangle, more than one triangle, or no triangle. (7.G.3) Describe t ...
Homework 27 Answers #1 Hint: Use the defect theorem 4.8.2. #2
... defect of each of these triangles is c, so c = c + c, which implies that c = 0. Because it is not possible to have a triangle with a defect of 0 in a hyperbolic geometry, then triangles in a hyperbolic geometry can't all have the same defect. 2. Let MN be the altitude of the Saccheri quadrilateral ...
... defect of each of these triangles is c, so c = c + c, which implies that c = 0. Because it is not possible to have a triangle with a defect of 0 in a hyperbolic geometry, then triangles in a hyperbolic geometry can't all have the same defect. 2. Let MN be the altitude of the Saccheri quadrilateral ...
Interactive Chalkboard
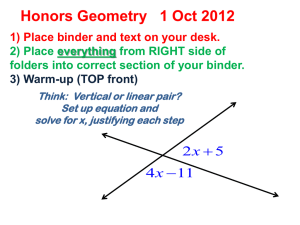
... ALGEBRA Find the measures of two complementary angles if one angle measures six degrees less than five times the measure of the other. ...
... ALGEBRA Find the measures of two complementary angles if one angle measures six degrees less than five times the measure of the other. ...