10.3 Inscribed Angles
... Using Inscribed Angles • An inscribed angle is an angle whose vertex is on a circle and whose sides contain chords of the circle. The arcinscribed angle that lies in the interior of an inscribed angle and ...
... Using Inscribed Angles • An inscribed angle is an angle whose vertex is on a circle and whose sides contain chords of the circle. The arcinscribed angle that lies in the interior of an inscribed angle and ...
6.4 Inscribed Angles
... Using Inscribed Angles • An inscribed angle is an angle whose vertex is on a circle and whose sides contain chords of the circle. The arcinscribed angle that lies in the interior of an inscribed angle and ...
... Using Inscribed Angles • An inscribed angle is an angle whose vertex is on a circle and whose sides contain chords of the circle. The arcinscribed angle that lies in the interior of an inscribed angle and ...
Triangles, Part 3
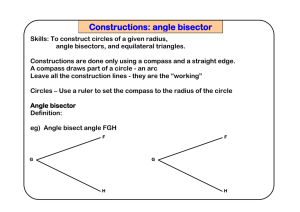
... into their binders. An angle bisector in a triangle is a line segment drawn from a vertex to the opposite side in which the line segment bisects the vertex angle. An interesting property of the three angle bisectors is that they meet at the same point. We will prove this later. Note this property. 1 ...
... into their binders. An angle bisector in a triangle is a line segment drawn from a vertex to the opposite side in which the line segment bisects the vertex angle. An interesting property of the three angle bisectors is that they meet at the same point. We will prove this later. Note this property. 1 ...
Lines and Angles
... 4. If two distinct planes intersect, then they intersect in exactly one line. ...
... 4. If two distinct planes intersect, then they intersect in exactly one line. ...