course title - Salmon School
... You will have daily assignments. These assignments will be worth 10-50 points each. All work must be shown or the student will take a zero for the assignment. These daily assignments are due the following day they are assigned at the beginning of class. Tests will be given at the end of each chapter ...
... You will have daily assignments. These assignments will be worth 10-50 points each. All work must be shown or the student will take a zero for the assignment. These daily assignments are due the following day they are assigned at the beginning of class. Tests will be given at the end of each chapter ...
Discrete Math Point, Line, Plane, Space
... Euclid’s 5 Postulates 5. That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles. ...
... Euclid’s 5 Postulates 5. That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles. ...
8. Hyperbolic triangles
... Note: This year, I’m not doing this material, apart from Pythagoras’ theorem, in the lectures (and, as such, the remainder isn’t examinable). I’ve left the material as Lecture 8 so that (i) anybody interested can read about hyperbolic trigonometry, and (ii) to save me having to renumber Lectures 9 o ...
... Note: This year, I’m not doing this material, apart from Pythagoras’ theorem, in the lectures (and, as such, the remainder isn’t examinable). I’ve left the material as Lecture 8 so that (i) anybody interested can read about hyperbolic trigonometry, and (ii) to save me having to renumber Lectures 9 o ...
0081_hsm11gmtr_01EM.indd
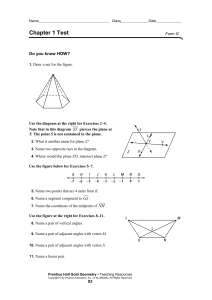
... Use the diagram at the right for Exercises 2–4. Note that in this diagram ST pierces the plane at T. The point S is not contained in the plane. 2. What is another name for plane Z? 3. Name two opposite rays in the diagram. 4. Where would the plane STL intersect plane Z? ...
... Use the diagram at the right for Exercises 2–4. Note that in this diagram ST pierces the plane at T. The point S is not contained in the plane. 2. What is another name for plane Z? 3. Name two opposite rays in the diagram. 4. Where would the plane STL intersect plane Z? ...
Enter the appropriate value to answer the question or solve the
... covers 110 m , how much will Mr. James need to spend to protect the storeroom? $_________ 16. Ranger Jill’s station is 18.3 miles due east of Ranger Will’s station. A fire is burning in the distance. ...
... covers 110 m , how much will Mr. James need to spend to protect the storeroom? $_________ 16. Ranger Jill’s station is 18.3 miles due east of Ranger Will’s station. A fire is burning in the distance. ...
Alabama COS Standards
... 2. Justify theorems related to pairs of angles, including angles formed by parallel and perpendicular lines, vertical angles, adjacent angles, complementary angles, and supplementary angles. Example: proving vertical angles congruent ...
... 2. Justify theorems related to pairs of angles, including angles formed by parallel and perpendicular lines, vertical angles, adjacent angles, complementary angles, and supplementary angles. Example: proving vertical angles congruent ...
File
... measures of interior angles of a triangle sum to 180; base angles of isosceles triangles are congruent; the segment joining the midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a point HSG-SRT.C.8 Use trigonometric ratios and t ...
... measures of interior angles of a triangle sum to 180; base angles of isosceles triangles are congruent; the segment joining the midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a point HSG-SRT.C.8 Use trigonometric ratios and t ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)