The point of concurrency of the three perpendicular bisectors of a
... path that has no thickness and extends forever The point that divides a segment into two congruent segments ...
... path that has no thickness and extends forever The point that divides a segment into two congruent segments ...
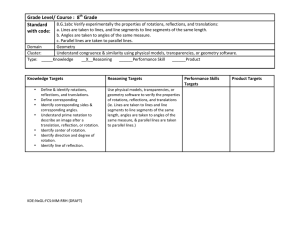
Geometry, Chapter 4: Congruent Triangles
... Describe, identify, label, name, recognize, explain, predict, differentiate, critique, justify, solve, apply, connect, construct ...
... Describe, identify, label, name, recognize, explain, predict, differentiate, critique, justify, solve, apply, connect, construct ...
Activity 5.5.1 The Angle Bisector Theorem
... 2. Observe that the length JK is the same as the lengths DE and DF. Now, use your mouse to drag point K around and observe what happens. What do you always notice about DE and DF? ...
... 2. Observe that the length JK is the same as the lengths DE and DF. Now, use your mouse to drag point K around and observe what happens. What do you always notice about DE and DF? ...
Angles Inside a Circle
... Lesson 9.6 Geometry Honors Objective: Student will be able to solve problems involving angles formed by chords, secants, and tangents. Page 357 ...
... Lesson 9.6 Geometry Honors Objective: Student will be able to solve problems involving angles formed by chords, secants, and tangents. Page 357 ...
Unit 2A 2013-14 - Youngstown City Schools
... shows the detail in proving the Pythagorean theorem. This activity can be done before showing the proof in class or after. After the Pythagorean theorem is proven, have students examine Pythagorean triples: 3-4-5, 5-12-13, 7-24-25, 8-15-17 and look at multiples of each triple. Also work on problems ...
... shows the detail in proving the Pythagorean theorem. This activity can be done before showing the proof in class or after. After the Pythagorean theorem is proven, have students examine Pythagorean triples: 3-4-5, 5-12-13, 7-24-25, 8-15-17 and look at multiples of each triple. Also work on problems ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)