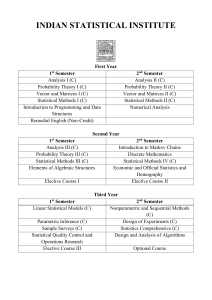
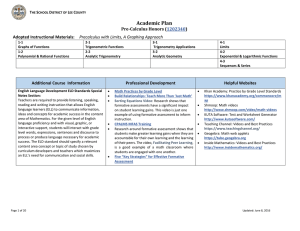
Structural Proof Theory
... the same as the logical task of controlling the correctness of a formal proof. We do not cover constructive type theory in detail, as another book would be needed for that, but some of the basic ideas and their connection to natural deduction and normalization procedures are explained in Appendix B. ...
... the same as the logical task of controlling the correctness of a formal proof. We do not cover constructive type theory in detail, as another book would be needed for that, but some of the basic ideas and their connection to natural deduction and normalization procedures are explained in Appendix B. ...
PhD Thesis First-Order Logic Investigation of Relativity Theory with
... method, but we can discover new, interesting and physically relevant theories. That happened in the case of the axiom of parallels in Euclid’s geometry; and this kind of investigation led to the discovery of hyperbolic geometry. Our FOL theory of accelerated observers (AccRel), which nicely fills th ...
... method, but we can discover new, interesting and physically relevant theories. That happened in the case of the axiom of parallels in Euclid’s geometry; and this kind of investigation led to the discovery of hyperbolic geometry. Our FOL theory of accelerated observers (AccRel), which nicely fills th ...
Predicate Logic
... Binding variables and scope When a quantifier is used on the variable x we say that this occurrence of x is bound. When the occurrence of a variable is not bound by a quantifier or set to a particular value, the variable is said to be free. The part of a logical expression to which a quantifier is a ...
... Binding variables and scope When a quantifier is used on the variable x we say that this occurrence of x is bound. When the occurrence of a variable is not bound by a quantifier or set to a particular value, the variable is said to be free. The part of a logical expression to which a quantifier is a ...
mathematical induction
... – Basis clause: T and F are propositional forms and if x V then x is a propositional form. – Inductive clause: If E1 and E2 are propositional forms then (E1), (E1 E2), (E1 E2), (E1 E2), (E1 E2) are all propositional forms. – Extremal clause: Nothing is a propositional form unless it is obt ...
... – Basis clause: T and F are propositional forms and if x V then x is a propositional form. – Inductive clause: If E1 and E2 are propositional forms then (E1), (E1 E2), (E1 E2), (E1 E2), (E1 E2) are all propositional forms. – Extremal clause: Nothing is a propositional form unless it is obt ...
Math Review for Algebra and Precalculus
... somewhat mechanical activities quickly and accurately. It’s very difficult to achieve this goal unless you understand how algebra works. Algebra is a symbolic language that allows communication between people who don’t know each others’ spoken language. The grammar of the language involves three mai ...
... somewhat mechanical activities quickly and accurately. It’s very difficult to achieve this goal unless you understand how algebra works. Algebra is a symbolic language that allows communication between people who don’t know each others’ spoken language. The grammar of the language involves three mai ...
Pattern 3
... When first encountering the symbol t n , it is natural to think that it means to multiply t by n since we often indicate multiplication by parentheses and writing two terms next to each other. For example, when we see 3 x 5 , we know that this means to distribute the 3 through the parenthes ...
... When first encountering the symbol t n , it is natural to think that it means to multiply t by n since we often indicate multiplication by parentheses and writing two terms next to each other. For example, when we see 3 x 5 , we know that this means to distribute the 3 through the parenthes ...
Ordinal Arithmetic
... Proving things directly with this definition is often awkward, since we have two di↵erent kinds of ordinals floating around — limits and successors. Thus the following form is often more convenient: Corollary 1.4 (Transfinite induction, practical form). Let P be a property of ordinals. If • (Base ca ...
... Proving things directly with this definition is often awkward, since we have two di↵erent kinds of ordinals floating around — limits and successors. Thus the following form is often more convenient: Corollary 1.4 (Transfinite induction, practical form). Let P be a property of ordinals. If • (Base ca ...
Principia Mathematica

The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913. In 1927, it appeared in a second edition with an important Introduction To the Second Edition, an Appendix A that replaced ✸9 and an all-new Appendix C.PM, as it is often abbreviated, was an attempt to describe a set of axioms and inference rules in symbolic logic from which all mathematical truths could in principle be proven. As such, this ambitious project is of great importance in the history of mathematics and philosophy, being one of the foremost products of the belief that such an undertaking may be achievable. However, in 1931, Gödel's incompleteness theorem proved definitively that PM, and in fact any other attempt, could never achieve this lofty goal; that is, for any set of axioms and inference rules proposed to encapsulate mathematics, either the system must be inconsistent, or there must in fact be some truths of mathematics which could not be deduced from them.One of the main inspirations and motivations for PM was the earlier work of Gottlob Frege on logic, which Russell discovered allowed for the construction of paradoxical sets. PM sought to avoid this problem by ruling out the unrestricted creation of arbitrary sets. This was achieved by replacing the notion of a general set with the notion of a hierarchy of sets of different 'types', a set of a certain type only allowed to contain sets of strictly lower types. Contemporary mathematics, however, avoids paradoxes such as Russell's in less unwieldy ways, such as the system of Zermelo–Fraenkel set theory.PM is not to be confused with Russell's 1903 Principles of Mathematics. PM states: ""The present work was originally intended by us to be comprised in a second volume of Principles of Mathematics... But as we advanced, it became increasingly evident that the subject is a very much larger one than we had supposed; moreover on many fundamental questions which had been left obscure and doubtful in the former work, we have now arrived at what we believe to be satisfactory solutions.""The Modern Library placed it 23rd in a list of the top 100 English-language nonfiction books of the twentieth century.