k-TO-l FUNCTIONS ON ARCS FOR k EVEN 1. eitherf((x,p))çz(f(x),f(p))
... sequence converging to q from the left is 0 and from the right is 1 (or the other way around). It was proved in Katsuura and Kellum [4] that each limit exists and is either 0 or 1. If both limits were 1, say, then there would be an interval of numbers (0, e) not mapped onto, contradicting the fact t ...
... sequence converging to q from the left is 0 and from the right is 1 (or the other way around). It was proved in Katsuura and Kellum [4] that each limit exists and is either 0 or 1. If both limits were 1, say, then there would be an interval of numbers (0, e) not mapped onto, contradicting the fact t ...
![[2014 solutions]](http://s1.studyres.com/store/data/008843334_1-6541359c94dca59dbb1b50426f79633e-300x300.png)
05 FX115 Ex Cmplx Num
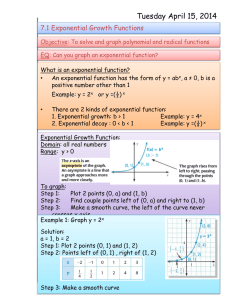
... look like? When you plot the points on a coordinate plane it doesn’t possess the same properties as a linear function or absolute value function. Students might say that it has some similar qualities of a quadratic function but it is not symmetrical. Nevertheless, an exponential function is rooted i ...
... look like? When you plot the points on a coordinate plane it doesn’t possess the same properties as a linear function or absolute value function. Students might say that it has some similar qualities of a quadratic function but it is not symmetrical. Nevertheless, an exponential function is rooted i ...
Class Notes 2 - Graphing and Writing Absolute Value Functions
... 2. Compare the function graph with the parent function graph and list the transforms that are apparent: - Magnitude of the slope of the branches? This will be the “a” value - Reflection across the x axis: Yes, we negate “a” - How has the x coordinate of the vertex changed from the parent (size & dir ...
... 2. Compare the function graph with the parent function graph and list the transforms that are apparent: - Magnitude of the slope of the branches? This will be the “a” value - Reflection across the x axis: Yes, we negate “a” - How has the x coordinate of the vertex changed from the parent (size & dir ...
January 2015
... In terms of x and y, for every x value there can be only one y value. If the table included (–4, 1) to the existing table that has the relation (–4, 2) There would exist two different outputs( 1 and 2), for the same input (–4 ) and that would not be consistent with the definition of a function. ...
... In terms of x and y, for every x value there can be only one y value. If the table included (–4, 1) to the existing table that has the relation (–4, 2) There would exist two different outputs( 1 and 2), for the same input (–4 ) and that would not be consistent with the definition of a function. ...
