On the Complexity of Qualitative Spatial Reasoning: A Maximal
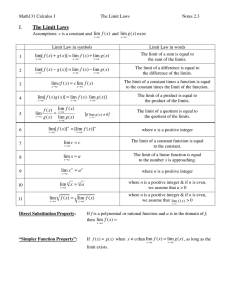
... Relationships between spatial regions are defined in terms of the relation C(a, b) which is true iff the closure of region a is connected to the closure of region b, i.e . if they share a common point. Regions themselves do not have to be internally connected, i.e . a single region may consist of di ...
... Relationships between spatial regions are defined in terms of the relation C(a, b) which is true iff the closure of region a is connected to the closure of region b, i.e . if they share a common point. Regions themselves do not have to be internally connected, i.e . a single region may consist of di ...
Notions of Computability at Higher Type
... §1. Introduction. This article is essentially a survey of fifty years of research on higher type computability. It was a great privilege to present much of this material in a series of three lectures at the Paris Logic Colloquium. In elementary recursion theory, one begins with the question: what do ...
... §1. Introduction. This article is essentially a survey of fifty years of research on higher type computability. It was a great privilege to present much of this material in a series of three lectures at the Paris Logic Colloquium. In elementary recursion theory, one begins with the question: what do ...
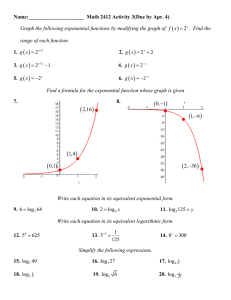
Modular Construction of Complete Coalgebraic Logics
... constant sets and composition. A recent survey of existing probabilistic models of systems [3] identified no less than eight probabilistic system types of interest, all of which can be written as such combinations. This paper derives logics and proof systems for these probabilistic system types, usi ...
... constant sets and composition. A recent survey of existing probabilistic models of systems [3] identified no less than eight probabilistic system types of interest, all of which can be written as such combinations. This paper derives logics and proof systems for these probabilistic system types, usi ...
AN EXPOSITION ANS DEVELOPMENT OF KANGER`S EARLY
... S ‚ ∀xϕ iff for every object a ∈ D, S(a/x) ‚ ϕ. Here, S(a/x) is the interpretation which is exactly like S, except for assigning the object a to the variable x as its value. Montague now asks the same question as Kanger: How can this definition of the truthrelation ‚ be generalized to first-order la ...
... S ‚ ∀xϕ iff for every object a ∈ D, S(a/x) ‚ ϕ. Here, S(a/x) is the interpretation which is exactly like S, except for assigning the object a to the variable x as its value. Montague now asks the same question as Kanger: How can this definition of the truthrelation ‚ be generalized to first-order la ...