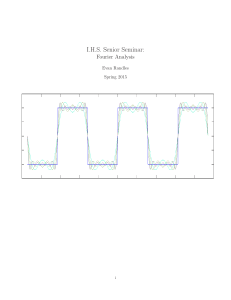
S5_Unit_1_ Outcome_2 - Cleveden Secondary School
... Defn: A function or mapping is a relationship between two sets in which each member of the first set is connected to exactly one member in the second set. If the first set is A and the second B then we often write ...
... Defn: A function or mapping is a relationship between two sets in which each member of the first set is connected to exactly one member in the second set. If the first set is A and the second B then we often write ...
Relation between chaos probability and zero
... of the harmonic oscillator. It is well known that the driven Duffing-like equation (4) can describe chaotic behavior [32]. So it is very hard to find an exact solution of this equation. However, when the driving strengths are weak enough, we can treat the chaotic system by the direct perturbation ap ...
... of the harmonic oscillator. It is well known that the driven Duffing-like equation (4) can describe chaotic behavior [32]. So it is very hard to find an exact solution of this equation. However, when the driving strengths are weak enough, we can treat the chaotic system by the direct perturbation ap ...
introduction to proofs
... E . Assume d , n ∈ Z+ . Because n is a multiple of d we have that n = d k for some k ∈ Z. Note that k ≥ 1 since otherwise n ≤ 0 but n is given as positive. Multiplying by the positive number d gives n = dk ≥ d. F . That every number is divisible by 1 follows from the fact that for every a ∈ Z the eq ...
... E . Assume d , n ∈ Z+ . Because n is a multiple of d we have that n = d k for some k ∈ Z. Note that k ≥ 1 since otherwise n ≤ 0 but n is given as positive. Multiplying by the positive number d gives n = dk ≥ d. F . That every number is divisible by 1 follows from the fact that for every a ∈ Z the eq ...
Polynomial and Rational Functions
... It turns out that there are direct, though complicated, methods for finding formulas for the zeros of any third- or fourth-degree polynomial function. However, the Frenchman Evariste Galois (1811–1832) proved at the age of 20 that for polynomial functions of degree greater than 4 there is no formula ...
... It turns out that there are direct, though complicated, methods for finding formulas for the zeros of any third- or fourth-degree polynomial function. However, the Frenchman Evariste Galois (1811–1832) proved at the age of 20 that for polynomial functions of degree greater than 4 there is no formula ...
Effectively Polynomial Simulations
... system is used as a SAT solver, polynomial-time preprocessing applied to the input formula could make the algorithm more effective. In fact, encoding problems (such as planning and inference) into SAT has become a huge subarea within artificial intelligence. It could be the case that effectively-p s ...
... system is used as a SAT solver, polynomial-time preprocessing applied to the input formula could make the algorithm more effective. In fact, encoding problems (such as planning and inference) into SAT has become a huge subarea within artificial intelligence. It could be the case that effectively-p s ...