Prime Factoriztion
... Gina is using acorns and leaves to make table centerpieces for a banquet. She wants each centerpiece to have the same number of acorns and the same number of leaves. She wants to use all the leaves and all the acorns. ...
... Gina is using acorns and leaves to make table centerpieces for a banquet. She wants each centerpiece to have the same number of acorns and the same number of leaves. She wants to use all the leaves and all the acorns. ...
GCF
... A. Finding the Greatest common Factor (GCF) of a List of Integers or a list of terms Greatest common Factor (GCF)—is the largest common factor of the integers in the list. Steps: 1. Write each of the numbers as a product of prime number using exponent for repeated number. 2. Identify the ...
... A. Finding the Greatest common Factor (GCF) of a List of Integers or a list of terms Greatest common Factor (GCF)—is the largest common factor of the integers in the list. Steps: 1. Write each of the numbers as a product of prime number using exponent for repeated number. 2. Identify the ...
History of Mathematics–Spring 2015
... FYI: The ratio AB/AC, known as the golden ratio and usually denoted by the Greek letter φ, appears in a lot of odd places. It appears a lot in the five pointed star or pentagram, which is obtained by drawing all the diagonals of a regular pentagon. It can be drawn without lifting the pen from the pa ...
... FYI: The ratio AB/AC, known as the golden ratio and usually denoted by the Greek letter φ, appears in a lot of odd places. It appears a lot in the five pointed star or pentagram, which is obtained by drawing all the diagonals of a regular pentagon. It can be drawn without lifting the pen from the pa ...
CMP3_G6_PT_AAG_3-2
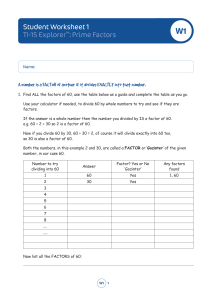
... factors for any number. For example, the prime factors of 330 are 2, 3, 5 and 11, and the prime factorization of 330 is 2 × 3 × 5 × 11. There is no other possible set of prime numbers that can be multiplied to make 330. The prime numbers cannot be broken down further into a product of primes. 3 can ...
... factors for any number. For example, the prime factors of 330 are 2, 3, 5 and 11, and the prime factorization of 330 is 2 × 3 × 5 × 11. There is no other possible set of prime numbers that can be multiplied to make 330. The prime numbers cannot be broken down further into a product of primes. 3 can ...












![THE RING Z[ √ D] - facstaff.bucknell.edu](http://s1.studyres.com/store/data/013114635_1-8d703d2c2f33989febabe1cd6c40a070-300x300.png)