Homework 9 Solutions
... (−10)5 ≡ 2 (mod 26), thus 16 · 5 ≡ 2 (mod 26). Hence x = 16. 4a) This is just like Example 4.9 in the book. We get the same values for x1 , x2 and x3 . Hence a solution is given by x = 1 · 35 · 2 + 2 · 21 · 1 + 3 · 15 · 1 = 157 ≡ 52 (mod 105). 4c) Here we have that n = 6 · 11 · 17 = 1122 We use the ...
... (−10)5 ≡ 2 (mod 26), thus 16 · 5 ≡ 2 (mod 26). Hence x = 16. 4a) This is just like Example 4.9 in the book. We get the same values for x1 , x2 and x3 . Hence a solution is given by x = 1 · 35 · 2 + 2 · 21 · 1 + 3 · 15 · 1 = 157 ≡ 52 (mod 105). 4c) Here we have that n = 6 · 11 · 17 = 1122 We use the ...
Unit 4 Review Problems Algebra 1 Answer Section
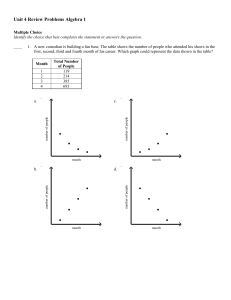
... ____ 30. The grocery store sells dates for $4.00 a pound and pomegranates for $2.75 a pound. Write an equation in standard form for the weights of dates d and pomegranates p that a customer could buy with $12. a. 4p + 2.75d = 12 c. 4d + 2.75p = 12 b. 4d = 2.75p + 12 d. 4 + 2.75 = d Write an equation ...
... ____ 30. The grocery store sells dates for $4.00 a pound and pomegranates for $2.75 a pound. Write an equation in standard form for the weights of dates d and pomegranates p that a customer could buy with $12. a. 4p + 2.75d = 12 c. 4d + 2.75p = 12 b. 4d = 2.75p + 12 d. 4 + 2.75 = d Write an equation ...