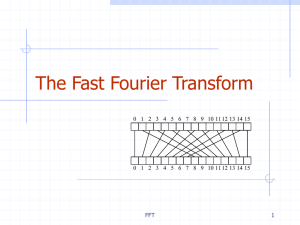
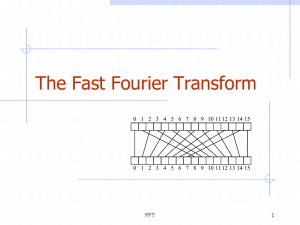
a(x) - Computer Science
... multiplication and modulo reduce answer • can do reduction at any point, ie – a+b mod n = [a mod n + b mod n] mod n ...
... multiplication and modulo reduce answer • can do reduction at any point, ie – a+b mod n = [a mod n + b mod n] mod n ...