2 - Set Theory
... It is just as important to know which objects are elements of a set as to know which objects are not elements of a set. If A ⊂ S, then we can define the complement of A in S as the set of all element in S that are not in A: A = {x ∈ S | x 6∈ A}. In other texts, complements may also be written as Ac ...
... It is just as important to know which objects are elements of a set as to know which objects are not elements of a set. If A ⊂ S, then we can define the complement of A in S as the set of all element in S that are not in A: A = {x ∈ S | x 6∈ A}. In other texts, complements may also be written as Ac ...
comments on the logic of constructible falsity (strong negation)
... Görnemann’s result suggests the conjecture that a classical model theory for the logic I have described may be obtained by allowing the domain to “grow with time”. This is in fact true. We may define a Nelson model structure as a triple (K, R, D), where K is a non-empty set of “stages of investigat ...
... Görnemann’s result suggests the conjecture that a classical model theory for the logic I have described may be obtained by allowing the domain to “grow with time”. This is in fact true. We may define a Nelson model structure as a triple (K, R, D), where K is a non-empty set of “stages of investigat ...
How Big Is Infinity?
... size as (i.e., there is a one-to-one correspondence between S and ), then the set is said to be countable. In other words, you can count the members of a countable set. The term denumerable is also used; it means the same as countable. ...
... size as (i.e., there is a one-to-one correspondence between S and ), then the set is said to be countable. In other words, you can count the members of a countable set. The term denumerable is also used; it means the same as countable. ...
pdf - Consequently.org
... fails the demand of consistency. This is one of the tests Belnap considers in the paper. In the case of a natural deduction proof theory or a sequent calculus, we can demonstrate that this criterion is met by means of a normalisation proof or a cut elimination argument, which usually has as a conseq ...
... fails the demand of consistency. This is one of the tests Belnap considers in the paper. In the case of a natural deduction proof theory or a sequent calculus, we can demonstrate that this criterion is met by means of a normalisation proof or a cut elimination argument, which usually has as a conseq ...
Comparing Constructive Arithmetical Theories Based - Math
... the intuitionistic deductive closure of BASIC), coN P induction does not imply N P induction; and that assuming the polynomial hierarchy does not collapse, neither does N P induction imply coN P induction. This is in sharp contrast to the case for classical logic, in which the two principles are equ ...
... the intuitionistic deductive closure of BASIC), coN P induction does not imply N P induction; and that assuming the polynomial hierarchy does not collapse, neither does N P induction imply coN P induction. This is in sharp contrast to the case for classical logic, in which the two principles are equ ...
Large cardinals and the Continuum Hypothesis
... finite subset B ⊆ A has a model, so does A. In order to generalize this property, we consider an extension of the classical logic denoted as Lκ,κ , where κ is a regular cardinal, as follows. A language in Lκ,κ can have up to κ many variables and an unlimited number of non-logical symbols (functions, ...
... finite subset B ⊆ A has a model, so does A. In order to generalize this property, we consider an extension of the classical logic denoted as Lκ,κ , where κ is a regular cardinal, as follows. A language in Lκ,κ can have up to κ many variables and an unlimited number of non-logical symbols (functions, ...
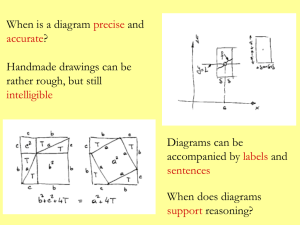
Diagrams in logic and mathematics - CFCUL
... 1. ontological statements are in general much more problematic than the difficulties they are intended to find solution to the infinite debate about the ontological nature of mathematical objects shows that it is very problematic to settle ontological questions once and for all Balaguer (1998) 2. ev ...
... 1. ontological statements are in general much more problematic than the difficulties they are intended to find solution to the infinite debate about the ontological nature of mathematical objects shows that it is very problematic to settle ontological questions once and for all Balaguer (1998) 2. ev ...
connections to higher type Recursion Theory, Proof-Theory
... using the given bijective pairing of numbers. However, since we are interested in higher type computations, as given by the HPEF, we need also other kinds of higher type objects, such as exponentiations, in the category. Unfortunately, there is no general way to enumerate the set of morphisms of two ...
... using the given bijective pairing of numbers. However, since we are interested in higher type computations, as given by the HPEF, we need also other kinds of higher type objects, such as exponentiations, in the category. Unfortunately, there is no general way to enumerate the set of morphisms of two ...
Document
... It is true since there is at least one real number x for which the proposition is true. Try x=2 Suppose that P is a propositional function whose domain of discourse consists of the elements d1,…,dn. The following pseudocode determines whether ...
... It is true since there is at least one real number x for which the proposition is true. Try x=2 Suppose that P is a propositional function whose domain of discourse consists of the elements d1,…,dn. The following pseudocode determines whether ...
Annals of Pure and Applied Logic Ordinal machines and admissible
... enumerable by an α -machine, respectively. We emphasize the algorithmic approach to admissible recursion theory by indicating how the proof of the Sacks–Simpson theorem, i.e., the solution of Post’s problem in α -recursion theory, could be based on α -machines, without involving constructibility the ...
... enumerable by an α -machine, respectively. We emphasize the algorithmic approach to admissible recursion theory by indicating how the proof of the Sacks–Simpson theorem, i.e., the solution of Post’s problem in α -recursion theory, could be based on α -machines, without involving constructibility the ...
Set theory
Set theory is the branch of mathematical logic that studies sets, which informally are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics. The language of set theory can be used in the definitions of nearly all mathematical objects.The modern study of set theory was initiated by Georg Cantor and Richard Dedekind in the 1870s. After the discovery of paradoxes in naive set theory, numerous axiom systems were proposed in the early twentieth century, of which the Zermelo–Fraenkel axioms, with the axiom of choice, are the best-known.Set theory is commonly employed as a foundational system for mathematics, particularly in the form of Zermelo–Fraenkel set theory with the axiom of choice. Beyond its foundational role, set theory is a branch of mathematics in its own right, with an active research community. Contemporary research into set theory includes a diverse collection of topics, ranging from the structure of the real number line to the study of the consistency of large cardinals.