4 The Cartesian Coordinate System - Pictures of Equa
... If a graph intersects the x-axis at the point (a, 0), then a is called an x-intercept of the graph. If a graph intersects the y-axis at the point (0, b), then b is called a y-intercept of the graph. Notice that the y value equals zero at an x-intercept and the x-value equals zero at a yintercept. ...
... If a graph intersects the x-axis at the point (a, 0), then a is called an x-intercept of the graph. If a graph intersects the y-axis at the point (0, b), then b is called a y-intercept of the graph. Notice that the y value equals zero at an x-intercept and the x-value equals zero at a yintercept. ...
Algebra Integrated with Statistics 3
... Use coordinates to prove simple geometric theorems algebraically - Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the ...
... Use coordinates to prove simple geometric theorems algebraically - Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the ...
Ohio Resource Center > Standards > Common Core > Mathematics
... Use coordinates to prove simple geometric theorems algebraically HSG-GPE.B.4 Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) li ...
... Use coordinates to prove simple geometric theorems algebraically HSG-GPE.B.4 Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) li ...
Unit 1 vocab part A
... is larger than 1, then the figure is enlarged. If the scale factor is between 0 and 1, then the figure is reduced. ...
... is larger than 1, then the figure is enlarged. If the scale factor is between 0 and 1, then the figure is reduced. ...
Common Core Learning Standards GRADE 8 Mathematics
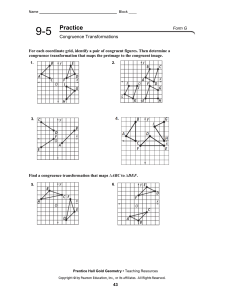
... figure is rotated, reflected, and/or translated. Describe the sequence of transformations that occurred from the original 2D figure to the image. Draw a reflection of an object. Draw a translation of an object. Draw a rotation of an object. Name corresponding parts in congruent figures. ...
... figure is rotated, reflected, and/or translated. Describe the sequence of transformations that occurred from the original 2D figure to the image. Draw a reflection of an object. Draw a translation of an object. Draw a rotation of an object. Name corresponding parts in congruent figures. ...
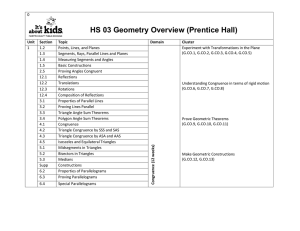
HS 03 Geometry Overview (Prentice Hall)
... Partitioning Segments into a Given Ratio Equations of Parabolas Using the Focus and Directrix Figures in the Coordinate Plane Proof in Coordinate Geometry Circles in the Coordinate Plane ...
... Partitioning Segments into a Given Ratio Equations of Parabolas Using the Focus and Directrix Figures in the Coordinate Plane Proof in Coordinate Geometry Circles in the Coordinate Plane ...
Geometry Standards
... Use coordinates to prove simple geometric theorems algebraically 4. Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the ...
... Use coordinates to prove simple geometric theorems algebraically 4. Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the ...
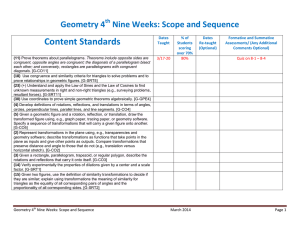
2nd 9 weeks
... G.GPE.5 Prove the slope criteria for parallel and perpendicular lines and uses them to solve geometric problems (e.g., find the equation of a line parallel or perpendicular to a given line that passes through a given point). ...
... G.GPE.5 Prove the slope criteria for parallel and perpendicular lines and uses them to solve geometric problems (e.g., find the equation of a line parallel or perpendicular to a given line that passes through a given point). ...
Lesson Plan Template - Trousdale County Schools
... a. Recognize opposite signs of numbers as indicating locations on opposite sides of 0 on the number line; recognize that the opposite of the opposite of a number is the number itself, e.g., –(–3) = 3, and that 0 is its own opposite. b. Understand signs of numbers in ordered pairs as indicating lo ...
... a. Recognize opposite signs of numbers as indicating locations on opposite sides of 0 on the number line; recognize that the opposite of the opposite of a number is the number itself, e.g., –(–3) = 3, and that 0 is its own opposite. b. Understand signs of numbers in ordered pairs as indicating lo ...
A Comparative study of the National Curriculum Statement
... Calculus: basic, largely intuitive understanding of derivatives and ability to apply them ...
... Calculus: basic, largely intuitive understanding of derivatives and ability to apply them ...
Chapter 1 Study Guide
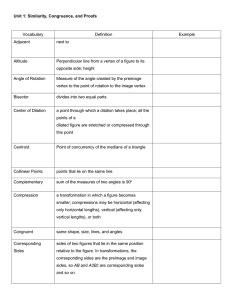
... 3. When two rays intersect with a common endpoint a(n) ________________ is formed. 4. The ________________ is the point located halfway between the endpoints of a segment. 5. ___________________ are nonadjacent angles formed by the intersection of two lines. 6. A(n) ________________ divides an angle ...
... 3. When two rays intersect with a common endpoint a(n) ________________ is formed. 4. The ________________ is the point located halfway between the endpoints of a segment. 5. ___________________ are nonadjacent angles formed by the intersection of two lines. 6. A(n) ________________ divides an angle ...
Cartesian coordinate system
A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis of the system, and the point where they meet is its origin, usually at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, n Cartesian coordinates (an element of real n-space) specify the point in an n-dimensional Euclidean space for any dimension n. These coordinates are equal, up to sign, to distances from the point to n mutually perpendicular hyperplanes.The invention of Cartesian coordinates in the 17th century by René Descartes (Latinized name: Cartesius) revolutionized mathematics by providing the first systematic link between Euclidean geometry and algebra. Using the Cartesian coordinate system, geometric shapes (such as curves) can be described by Cartesian equations: algebraic equations involving the coordinates of the points lying on the shape. For example, a circle of radius 2 in a plane may be described as the set of all points whose coordinates x and y satisfy the equation x2 + y2 = 4.Cartesian coordinates are the foundation of analytic geometry, and provide enlightening geometric interpretations for many other branches of mathematics, such as linear algebra, complex analysis, differential geometry, multivariate calculus, group theory and more. A familiar example is the concept of the graph of a function. Cartesian coordinates are also essential tools for most applied disciplines that deal with geometry, including astronomy, physics, engineering and many more. They are the most common coordinate system used in computer graphics, computer-aided geometric design and other geometry-related data processing.