Postulates and Theorems - Sleepy Eye Public Schools
... *Triangle Angle-Sum Theorem: The sum of the measures of the angles of a triangle is 180. *Triangle Exterior Angle Theorem: The measure of each exterior angle of a triangle equals the sum of the measures of its two remote interior angles. *Corollary to the Triangle Exterior Angle Theorem: The measure ...
... *Triangle Angle-Sum Theorem: The sum of the measures of the angles of a triangle is 180. *Triangle Exterior Angle Theorem: The measure of each exterior angle of a triangle equals the sum of the measures of its two remote interior angles. *Corollary to the Triangle Exterior Angle Theorem: The measure ...
Geometry Semester 1 Instructional Materials
... 12. Choose one of the following to complete the proof. A. Definition of angle bisector- If a ray is an angle bisector, then it divides an angle into two congruent angles. B. Definition of opposite rays- If a point on the line determines two rays are collinear, then the rays are opposite rays. C. Def ...
... 12. Choose one of the following to complete the proof. A. Definition of angle bisector- If a ray is an angle bisector, then it divides an angle into two congruent angles. B. Definition of opposite rays- If a point on the line determines two rays are collinear, then the rays are opposite rays. C. Def ...
Geometry, 4.2 Notes –Proofs with no Diagrams
... • Sketch the problem out first to visualize what is being said. • Find the ‘verb’ or ‘action word’ (is, bisects, divides, etc.) • Look at the words after the action word. This is part of what you want to prove. • Find what is doing the action…this is also part of what you want to prove. • Look at th ...
... • Sketch the problem out first to visualize what is being said. • Find the ‘verb’ or ‘action word’ (is, bisects, divides, etc.) • Look at the words after the action word. This is part of what you want to prove. • Find what is doing the action…this is also part of what you want to prove. • Look at th ...
Math Prep 3 Answer Key
... 29) The arch above is constructed of 5 nearly congruent stones, each of which is in the shape of a right prism with trapezoid bases. Based on the approximate measurements provided, which of the following best approximates the volume of the entire arch? ...
... 29) The arch above is constructed of 5 nearly congruent stones, each of which is in the shape of a right prism with trapezoid bases. Based on the approximate measurements provided, which of the following best approximates the volume of the entire arch? ...
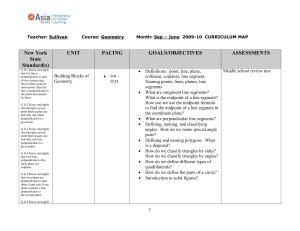
Mohawk Local Schools Geometry Quarter 2 Curriculum Guide
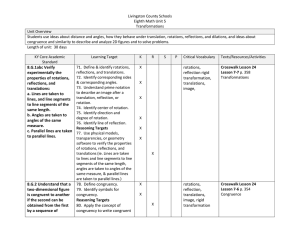
... transformations that were used to carry the given figure onto the other. (R) Recall previous understandings of coordinate geometry (including, but not limited to: distance, midpoint and slope formula, equation of a line, definitions of parallel and perpendicular lines, etc.) (K) Use coordinates to p ...
... transformations that were used to carry the given figure onto the other. (R) Recall previous understandings of coordinate geometry (including, but not limited to: distance, midpoint and slope formula, equation of a line, definitions of parallel and perpendicular lines, etc.) (K) Use coordinates to p ...
Non-Euclidean Geometry
... Definition 3. A pencil of lines consists of all lines which (i) intersect in a common point; (ii) are parallel to a given line; or (iii) have a common perpendicular. Let x, y be two lines of a pencil. Then if x and y intersect in a point P , the product σy σx is a “rotation” ρP,α about the point P t ...
... Definition 3. A pencil of lines consists of all lines which (i) intersect in a common point; (ii) are parallel to a given line; or (iii) have a common perpendicular. Let x, y be two lines of a pencil. Then if x and y intersect in a point P , the product σy σx is a “rotation” ρP,α about the point P t ...
Geometry Definitions
... protractor - Instrument used to determine the measure of an angle in degrees. prove - Conclusion to be reached in a proof. ...
... protractor - Instrument used to determine the measure of an angle in degrees. prove - Conclusion to be reached in a proof. ...
1 Lecture 7 THE POINCARÉ DISK MODEL OF HYPERBOLIC
... 7.8. Hyperbolic geometry and the physical world In his famous book Science et Hypothèse, Henri Poincaré describes the physics of a small “universe” and the physical theories that its inhabitants would create. The universe considered by Poincaré is Euclidean, plane (twodimensional), has the form o ...
... 7.8. Hyperbolic geometry and the physical world In his famous book Science et Hypothèse, Henri Poincaré describes the physics of a small “universe” and the physical theories that its inhabitants would create. The universe considered by Poincaré is Euclidean, plane (twodimensional), has the form o ...
NM3M03AAA.pdf - Mira Costa High School
... a. Line(s) parallel to AF and containing point E b. Line(s) skew to AF and containing point E c. Line(s) perpendicular to AF and containing point E d. Plane(s) parallel to plane FGH and containing point E ...
... a. Line(s) parallel to AF and containing point E b. Line(s) skew to AF and containing point E c. Line(s) perpendicular to AF and containing point E d. Plane(s) parallel to plane FGH and containing point E ...
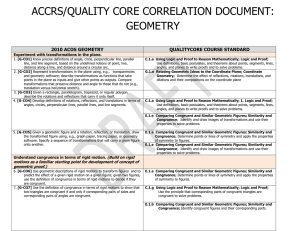
ACCRS/QualityCore-Geometry Correlation - UPDATED
... C.1.e Using Logic and Proof to Reason Mathematically; Logic and Proof; Read and write different types and formats of proofs including two-column, flowchart, paragraph, and indirect proofs. C.1.i Using Logic and Proof to Reason Mathematically; Logic and Proof; Use properties of special quadrilateral ...
... C.1.e Using Logic and Proof to Reason Mathematically; Logic and Proof; Read and write different types and formats of proofs including two-column, flowchart, paragraph, and indirect proofs. C.1.i Using Logic and Proof to Reason Mathematically; Logic and Proof; Use properties of special quadrilateral ...
Cartesian coordinate system
A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis of the system, and the point where they meet is its origin, usually at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, n Cartesian coordinates (an element of real n-space) specify the point in an n-dimensional Euclidean space for any dimension n. These coordinates are equal, up to sign, to distances from the point to n mutually perpendicular hyperplanes.The invention of Cartesian coordinates in the 17th century by René Descartes (Latinized name: Cartesius) revolutionized mathematics by providing the first systematic link between Euclidean geometry and algebra. Using the Cartesian coordinate system, geometric shapes (such as curves) can be described by Cartesian equations: algebraic equations involving the coordinates of the points lying on the shape. For example, a circle of radius 2 in a plane may be described as the set of all points whose coordinates x and y satisfy the equation x2 + y2 = 4.Cartesian coordinates are the foundation of analytic geometry, and provide enlightening geometric interpretations for many other branches of mathematics, such as linear algebra, complex analysis, differential geometry, multivariate calculus, group theory and more. A familiar example is the concept of the graph of a function. Cartesian coordinates are also essential tools for most applied disciplines that deal with geometry, including astronomy, physics, engineering and many more. They are the most common coordinate system used in computer graphics, computer-aided geometric design and other geometry-related data processing.