![[pdf]](http://s1.studyres.com/store/data/008845329_1-93e98d576f966fb1eddead1ee71a18db-300x300.png)
[pdf]
... • However, the structure of these algorithms is similar: MVM is the key operation. • Major area of research in numerical analysis: speeding up iterative algorithms further by preconditioning. ...
... • However, the structure of these algorithms is similar: MVM is the key operation. • Major area of research in numerical analysis: speeding up iterative algorithms further by preconditioning. ...
Linear codes, generator matrices, check matrices, cyclic codes
... Proof: On one hand, the collection of polynomial multiples of b(x), reduced mod xn − 1, certainly includes multiples of p(x) reduced mod xn − 1, since p(x) is a multiple of b(x). On the other hand, since a(x) is relatively prime to xn − 1, it has an inverse i(x) modulo xn − 1. For any polynomial r(x ...
... Proof: On one hand, the collection of polynomial multiples of b(x), reduced mod xn − 1, certainly includes multiples of p(x) reduced mod xn − 1, since p(x) is a multiple of b(x). On the other hand, since a(x) is relatively prime to xn − 1, it has an inverse i(x) modulo xn − 1. For any polynomial r(x ...
Reformulated as: either all Mx = b are solvable, or Mx = 0 has
... 2.9.2. The inverse of a linear transformation. Let T : U ! V be a linear transformation between two vector spaces U and V . If T is onto to one and onto, then the function T has an inverse T 1 , T 1 : V ! U . Exercise. Show that the inverse of a linear transformation is also a linear transformation. ...
... 2.9.2. The inverse of a linear transformation. Let T : U ! V be a linear transformation between two vector spaces U and V . If T is onto to one and onto, then the function T has an inverse T 1 , T 1 : V ! U . Exercise. Show that the inverse of a linear transformation is also a linear transformation. ...
SOMEWHAT STOCHASTIC MATRICES 1. Introduction. The notion
... Suppose that P is a stochastic matrix with all positive entries. Then there exists a unique probability vector q such that P q = q. If {xk } is a Markov chain determined by P , then it converges to q. More generally, the same conclusion holds for a stochastic matrix P for which P s has all positive ...
... Suppose that P is a stochastic matrix with all positive entries. Then there exists a unique probability vector q such that P q = q. If {xk } is a Markov chain determined by P , then it converges to q. More generally, the same conclusion holds for a stochastic matrix P for which P s has all positive ...
4.19.1. Theorem 4.20
... Consider the linear transformation T : R n R n such that m T A aij relative to the basis of unit coordinate vectors. Given x such that T x O , let X be the n 1 column matrix that corresponds to x. We have AX 0 , where 0 is the zero column matrix. Thus, B AX 0 for any n ...
... Consider the linear transformation T : R n R n such that m T A aij relative to the basis of unit coordinate vectors. Given x such that T x O , let X be the n 1 column matrix that corresponds to x. We have AX 0 , where 0 is the zero column matrix. Thus, B AX 0 for any n ...
Introduction and Examples Matrix Addition and
... Introduction and Examples DEFINITION: A matrix is defined as an ordered rectangular array of numbers. They can be used to represent systems of linear equations, as will be explained below Here are a couple of examples of different types of matrices: Symmetric ...
... Introduction and Examples DEFINITION: A matrix is defined as an ordered rectangular array of numbers. They can be used to represent systems of linear equations, as will be explained below Here are a couple of examples of different types of matrices: Symmetric ...
A( v)
... When we learn PCA (Principal Component Analysis), we’ll know how to find these axes that minimize the sum of distances2 ...
... When we learn PCA (Principal Component Analysis), we’ll know how to find these axes that minimize the sum of distances2 ...
Summary of week 8 (Lectures 22, 23 and 24) This week we
... hence there exists at least one eigenvalue and a corresponding eigenvector. There exists an invertible matrix T such that T −1 AT is diagonal if and only if it is possible to find n linearly independent eigenvectors. This can always be done it A is symmetric, but non-symmetric matrices are not neces ...
... hence there exists at least one eigenvalue and a corresponding eigenvector. There exists an invertible matrix T such that T −1 AT is diagonal if and only if it is possible to find n linearly independent eigenvectors. This can always be done it A is symmetric, but non-symmetric matrices are not neces ...
Elementary Matrix Operations and Elementary Matrices
... Change of Coordinates for Left-Multiplication Transformations ...
... Change of Coordinates for Left-Multiplication Transformations ...
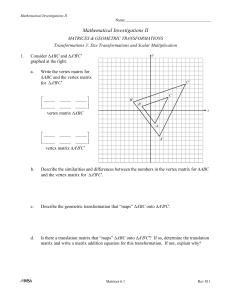
6.4 Dilations
... You should have noticed that in mapping ABC onto A'B'C', all of coordinates were doubled in the first problem and all of the coordinates were halved in the second problem. In addition, it should have been clear that there is no translation matrix that maps ABC onto A'B'C' because the two triangl ...
... You should have noticed that in mapping ABC onto A'B'C', all of coordinates were doubled in the first problem and all of the coordinates were halved in the second problem. In addition, it should have been clear that there is no translation matrix that maps ABC onto A'B'C' because the two triangl ...
8.1 and 8.2 - Shelton State
... The rows of a matrix are horizontal. The columns of a matrix are vertical. The matrix shown has 2 rows and 3 columns. A matrix with m rows and n columns is said to be of order m n. When m = n the matrix is said to be square. See Example 1, page 783. ...
... The rows of a matrix are horizontal. The columns of a matrix are vertical. The matrix shown has 2 rows and 3 columns. A matrix with m rows and n columns is said to be of order m n. When m = n the matrix is said to be square. See Example 1, page 783. ...
Chapter 3
... Theorem 3.4. For A an n × n matrix, the following are equivalent: (i) A is invertible; (ii) AX = 0n×1 has only the trivial solution X = 0n×1 ; (iii) the reduced row echelon form of A is In ; (iv) A is row equivalent to In ; (v) A can be written as a product of elementary matrices. Proof. We prove (i ...
... Theorem 3.4. For A an n × n matrix, the following are equivalent: (i) A is invertible; (ii) AX = 0n×1 has only the trivial solution X = 0n×1 ; (iii) the reduced row echelon form of A is In ; (iv) A is row equivalent to In ; (v) A can be written as a product of elementary matrices. Proof. We prove (i ...