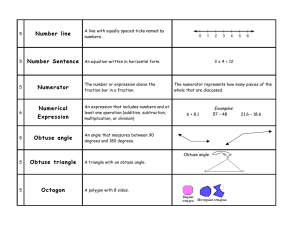
Geometric Numbers
... Exactly like a multiplication chart, we can use the same idea for square numbers! Notice how the square numbers line up along the diagonal… ...
... Exactly like a multiplication chart, we can use the same idea for square numbers! Notice how the square numbers line up along the diagonal… ...
Pythagorean Theorem Since we square the numbers in the
... _________________________ Since we square the numbers in the Pythagorean Theorem, let’s review squaring and taking the square root. When we square a number, we multiply the base times itself. Practice: 1) 22 = _____ ...
... _________________________ Since we square the numbers in the Pythagorean Theorem, let’s review squaring and taking the square root. When we square a number, we multiply the base times itself. Practice: 1) 22 = _____ ...
How_To_Multiply - DEP
... • 2-To multiply two digit numbers having tenth place digits same and the sum of unit place numbers are 10. • 3-Multiplying two , two digit numbers ,where difference between them is 10 & 5 in their unit place. • 4-To multiply two digit numbers in which either unit place or tenth place numbers are sam ...
... • 2-To multiply two digit numbers having tenth place digits same and the sum of unit place numbers are 10. • 3-Multiplying two , two digit numbers ,where difference between them is 10 & 5 in their unit place. • 4-To multiply two digit numbers in which either unit place or tenth place numbers are sam ...
Real Numbers and the Number Line
... A Radicand is the number under the radical symbol (sometimes called square root sign) A “radical” is just a number written in the form of a radical symbol and a radicand. ...
... A Radicand is the number under the radical symbol (sometimes called square root sign) A “radical” is just a number written in the form of a radical symbol and a radicand. ...
Notes on mathematics related to the `buzz contest`.
... algorithms that test for primality. If all we want is an answer that is probably correct, then there are even faster algorithms. Fermat’s (little) theorem, saying that ap−1 ≡ 1 (mod p) is the key here, but there are twists which improve on it. For instance, a(p−1)/2 ≡ ±1 (mod p). Most non-primes fai ...
... algorithms that test for primality. If all we want is an answer that is probably correct, then there are even faster algorithms. Fermat’s (little) theorem, saying that ap−1 ≡ 1 (mod p) is the key here, but there are twists which improve on it. For instance, a(p−1)/2 ≡ ±1 (mod p). Most non-primes fai ...