appendix A
... A radix k number system requires ___ different symbols to represent the digits ___________. ...
... A radix k number system requires ___ different symbols to represent the digits ___________. ...
Subtracting Fractions
... Subtracting Fractions Fractions are just like decimals, they are parts of a whole number and they look like this ⅝. There are two parts to every fraction. There’s the ...
... Subtracting Fractions Fractions are just like decimals, they are parts of a whole number and they look like this ⅝. There are two parts to every fraction. There’s the ...
Scope and Sequence - year 9 - mathsyear7-12
... They comprehend that irrational numbers have an infinite non-terminating decimal form. They specify decimal rational approximations for square roots of primes, rational numbers that are not perfect squares, the golden ratio φ , and simple fractions of π correct to a required decimal place accuracy. ...
... They comprehend that irrational numbers have an infinite non-terminating decimal form. They specify decimal rational approximations for square roots of primes, rational numbers that are not perfect squares, the golden ratio φ , and simple fractions of π correct to a required decimal place accuracy. ...
Second Year Honours Maths Notes on Factors
... Open up two brackets Break up the x2 into x and x and put each into the beginning of each bracket. Then break up the end number into factors and put your answers into the end of each bracket. If the second sign is + then both signs will be the same and if the second sign is – then both signs ...
... Open up two brackets Break up the x2 into x and x and put each into the beginning of each bracket. Then break up the end number into factors and put your answers into the end of each bracket. If the second sign is + then both signs will be the same and if the second sign is – then both signs ...
Gr. 5 Math: Unit 2 - Algebra
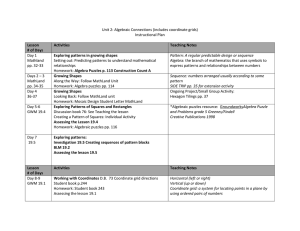
... Graphing Patterns on a Grid: Describe location and movement on coordinate grid D.B. 74 (toothpick patterns on a grid) Student book pp.246 Practice Homework: pp. 247 Using a graph to Generalize a Rule Reading a line graph and redrawing a line graph D.B. pp. 75 B.L.M. 19.2 Assessing the lesson Homewor ...
... Graphing Patterns on a Grid: Describe location and movement on coordinate grid D.B. 74 (toothpick patterns on a grid) Student book pp.246 Practice Homework: pp. 247 Using a graph to Generalize a Rule Reading a line graph and redrawing a line graph D.B. pp. 75 B.L.M. 19.2 Assessing the lesson Homewor ...