Measurement - tamchemistryhart
... • We will also talk about how to gauge the accuracy and precision of our measurements. ...
... • We will also talk about how to gauge the accuracy and precision of our measurements. ...
Extra Practice
... Scientific notation presents an easier way to write very large and very small numbers. Instead of writing 67,000,000,000, we use a power notation. We write 6.7 x 10 10. 6.7 is the coefficient – always a number between 1 and 10. 10 is the base. The superscript 10 means that the decimal point is 10 sp ...
... Scientific notation presents an easier way to write very large and very small numbers. Instead of writing 67,000,000,000, we use a power notation. We write 6.7 x 10 10. 6.7 is the coefficient – always a number between 1 and 10. 10 is the base. The superscript 10 means that the decimal point is 10 sp ...
Interactive Study Guide for Students: Trigonometric Functions
... An expression like 2222 can be written as a __________. A power Write each expression using has two parts, a _________ and an ______________. An exponent is a exponents. shorter way of writing repeated multiplication. So 2222 can be ...
... An expression like 2222 can be written as a __________. A power Write each expression using has two parts, a _________ and an ______________. An exponent is a exponents. shorter way of writing repeated multiplication. So 2222 can be ...
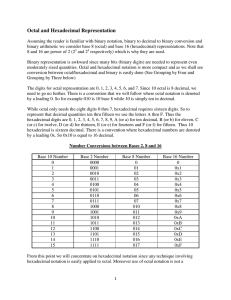
Octal and Hexadecimal Representation
... 8 and 16 are power of 2 (23 and 24 respectively) which is why they are used. Binary representation is awkward since many bits (binary digits) are needed to represent even moderately sized quantities. Octal and hexadecimal notation is more compact and as we shall see conversion between octal/hexadeci ...
... 8 and 16 are power of 2 (23 and 24 respectively) which is why they are used. Binary representation is awkward since many bits (binary digits) are needed to represent even moderately sized quantities. Octal and hexadecimal notation is more compact and as we shall see conversion between octal/hexadeci ...
Full tex
... [8], McCranie, [1], and Nash [5]. Several examples have been found of hyperperfect numbers with two, three and four different prime factors and one such number with five different prime factors was discovered be te Riele [8]. In this paper we include some new hyperperfect numbers with five different ...
... [8], McCranie, [1], and Nash [5]. Several examples have been found of hyperperfect numbers with two, three and four different prime factors and one such number with five different prime factors was discovered be te Riele [8]. In this paper we include some new hyperperfect numbers with five different ...