SODA 6C1 - Teachinglinks.net
... 1. What proportion of square numbers are even? 2. An even square number < 30 3. List the factors of the 8th square number 4. Draw a pair of (exactly) parallel lines. 5. 70 x 70 6. What do I multiply 70 by to get 7000? 7. A race is 10000 m. How many km is this? 8. How many mm is 4.6 cm? 9. Draw a lin ...
... 1. What proportion of square numbers are even? 2. An even square number < 30 3. List the factors of the 8th square number 4. Draw a pair of (exactly) parallel lines. 5. 70 x 70 6. What do I multiply 70 by to get 7000? 7. A race is 10000 m. How many km is this? 8. How many mm is 4.6 cm? 9. Draw a lin ...
Maths Calculation Booklet - Henry Chichele Primary School
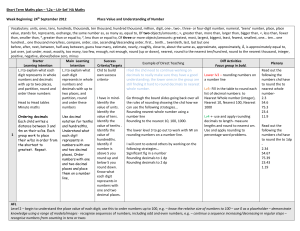
... Progression from mental to written calculations – why? Teaching throughout the school is progressive. Pupils develop their understanding in the four different operations, addition, subtraction, multiplication and division. With the new curriculum expectations, pupils need to be able to explain and ...
... Progression from mental to written calculations – why? Teaching throughout the school is progressive. Pupils develop their understanding in the four different operations, addition, subtraction, multiplication and division. With the new curriculum expectations, pupils need to be able to explain and ...
Working with Very Large and Very Small Numbers
... Working with Very Large and Very Small Numbers Very large and very small numbers can be expressed in scientific |a| means all positive notation. In general, a number is expressed in scientific notation as: values of a. For any n a × 10 , where 1 ≤ |a| ≤ 9 and n is a positive or negative integer. T ...
... Working with Very Large and Very Small Numbers Very large and very small numbers can be expressed in scientific |a| means all positive notation. In general, a number is expressed in scientific notation as: values of a. For any n a × 10 , where 1 ≤ |a| ≤ 9 and n is a positive or negative integer. T ...
Section 4.3 - math-clix
... then the result f(c) is the remainder that would be obtained by dividing f(x) by x c. That is, if f(x) = (x c) • Q(x) + R, then f(c) = R. ...
... then the result f(c) is the remainder that would be obtained by dividing f(x) by x c. That is, if f(x) = (x c) • Q(x) + R, then f(c) = R. ...
Reat Numbers and Their Properties
... This notation is read "The set of all numbersof the formalb such that a and b are integerswith b not equal to zero." ln our set notationwe used lettersto representintegers.A letter that is usedto representa numberis called a variable. Thereare infinitely many rationalnumberslocatedbetweeneachpair of ...
... This notation is read "The set of all numbersof the formalb such that a and b are integerswith b not equal to zero." ln our set notationwe used lettersto representintegers.A letter that is usedto representa numberis called a variable. Thereare infinitely many rationalnumberslocatedbetweeneachpair of ...
Maths 59 - Worldlink Academy
... 19. The average of two numbers is xy. If one number is equal to x, the other number is equal to: ...
... 19. The average of two numbers is xy. If one number is equal to x, the other number is equal to: ...
Converse of the Pythagorean Theorem
... relationship called the Pythagorean Theorem is named for Pythagoras, a Greek mathematician who lived in the sixth century b.c. We now know that the Babylonians, Egyptians, and Chinese were aware of this relationship before its discovery by Pythagoras. ...
... relationship called the Pythagorean Theorem is named for Pythagoras, a Greek mathematician who lived in the sixth century b.c. We now know that the Babylonians, Egyptians, and Chinese were aware of this relationship before its discovery by Pythagoras. ...
MEYL624 TUTOR NOTES Module 2
... It gives the positive square roots for all non-negative numbers. It gives an error message for negative ones because you cannot have a (real) square root for a negative number. When x > 1 the square root is less than x, when x = 1 the square root equals 1, for 1 > x > 0 the answer is larger than x, ...
... It gives the positive square roots for all non-negative numbers. It gives an error message for negative ones because you cannot have a (real) square root for a negative number. When x > 1 the square root is less than x, when x = 1 the square root equals 1, for 1 > x > 0 the answer is larger than x, ...