Problem_Set_04
... a. Every binary string contains identical symbols. The proof is by induction on the size of the string. For n=0 all binary strings are empty and therefore identical. Let X = bnbn-1…b1b0 be an arbitrary binary string of length n+1. Let Y = bnbn-1…b1 and Z = bn-1…b1b0. Since both Y and Z are strings o ...
... a. Every binary string contains identical symbols. The proof is by induction on the size of the string. For n=0 all binary strings are empty and therefore identical. Let X = bnbn-1…b1b0 be an arbitrary binary string of length n+1. Let Y = bnbn-1…b1 and Z = bn-1…b1b0. Since both Y and Z are strings o ...
digital logic design
... achieved by using parity bits. A parity bit is an extra bit included with a message to make the total number of 1's ...
... achieved by using parity bits. A parity bit is an extra bit included with a message to make the total number of 1's ...
Irrational Numbers - Hewlett
... the full story! It actually goes on and on, with no pattern to the numbers. You cannot write down a simple fraction that equals the square root of 2. So the square root of 2 is an irrational number When dealing with square roots a lot of them are classified as IRRATIONAL numbers. The special few tha ...
... the full story! It actually goes on and on, with no pattern to the numbers. You cannot write down a simple fraction that equals the square root of 2. So the square root of 2 is an irrational number When dealing with square roots a lot of them are classified as IRRATIONAL numbers. The special few tha ...
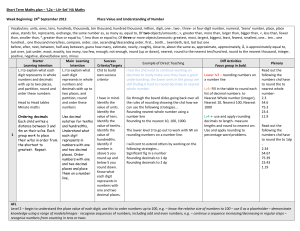
Estimating Notes - Moore Middle School
... 1-2 Estimating with Whole Numbers Sometimes in math you do not need an exact answer. Instead, you can use an estimate. Estimates are close to the exact answer but are usually easier and faster to find. When estimating, you can round the numbers in the problem to compatible numbers. Compatible numbe ...
... 1-2 Estimating with Whole Numbers Sometimes in math you do not need an exact answer. Instead, you can use an estimate. Estimates are close to the exact answer but are usually easier and faster to find. When estimating, you can round the numbers in the problem to compatible numbers. Compatible numbe ...