Matrices and Linear Functions
... That is, the composition of two linear functions is another linear function and we can compute the matrix of the composition from the matrices of the functions being composed. This is our motivation for defining the product of the matrices A and B, AB, by AB = C where C is as given in (3). It is imp ...
... That is, the composition of two linear functions is another linear function and we can compute the matrix of the composition from the matrices of the functions being composed. This is our motivation for defining the product of the matrices A and B, AB, by AB = C where C is as given in (3). It is imp ...
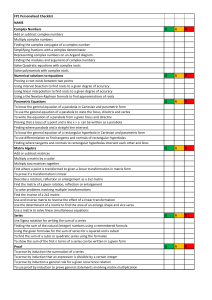
Matrix Vocabulary
... *In order to multiply two matrices, the # of columns of the first matrix must equal the number of rows of the second. To determine if it is possible to multiply two matrices check the number of columns of the first matrix with the rows of the second (The inside numbers): ...
... *In order to multiply two matrices, the # of columns of the first matrix must equal the number of rows of the second. To determine if it is possible to multiply two matrices check the number of columns of the first matrix with the rows of the second (The inside numbers): ...