Real Numbers, Exponents, and Scientific Notation
... a. If x is the length of one side of the painting, what equation can you set up to find the length of a side? b. Solve the equation you wrote in part a. How many solutions does the equation have? ...
... a. If x is the length of one side of the painting, what equation can you set up to find the length of a side? b. Solve the equation you wrote in part a. How many solutions does the equation have? ...
Rational Numbers (Decimals)
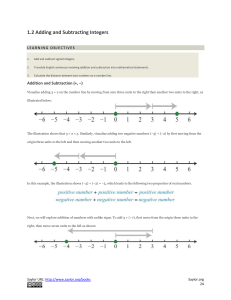
... In the diagram below, fill in the number of the highlighted line (above) that corresponds to the detail that has been pointed out. Two have been completed, so be sure to understand those answers before you begin! • Line 5 is upgrading the group of 10 ones in 12 (i.e. we are “carrying” one ten). • Li ...
... In the diagram below, fill in the number of the highlighted line (above) that corresponds to the detail that has been pointed out. Two have been completed, so be sure to understand those answers before you begin! • Line 5 is upgrading the group of 10 ones in 12 (i.e. we are “carrying” one ten). • Li ...
BARENDREGT`S LEMMA Dedicated to Henk Barendregt, in
... It is a statement that needs careful reading in order to grasp it. Jokingly, and with some exaggeration, we would sometimes refer to it as that lemma that is almost as difficult to formulate as it is to prove. As to the quoted proof, “Same method as the proof of 9” says so much as: by the method use ...
... It is a statement that needs careful reading in order to grasp it. Jokingly, and with some exaggeration, we would sometimes refer to it as that lemma that is almost as difficult to formulate as it is to prove. As to the quoted proof, “Same method as the proof of 9” says so much as: by the method use ...
Document
... 4. The bleachers at a football game is 7/8 full, and half the fans are rooting for the home team. What fraction of the bleacher is rooting for the home team? ...
... 4. The bleachers at a football game is 7/8 full, and half the fans are rooting for the home team. What fraction of the bleacher is rooting for the home team? ...
Chapter 2: Limits and Continuity
... Continuity Continuity at a Point The basic idea is as follows: We are given a function f and a number c. We calculate (if we can) both lim f x and f (c). If these two numbers are equal, we x c say that f is continuous at c. Here is the definition formally stated. ...
... Continuity Continuity at a Point The basic idea is as follows: We are given a function f and a number c. We calculate (if we can) both lim f x and f (c). If these two numbers are equal, we x c say that f is continuous at c. Here is the definition formally stated. ...
romping in numberland
... come across peculiarities, make a note of them and just forget about them for the present. You may treat them as curies or freaks just as you do when you see a person with more than five fingers in a hand. If a certain pattern repeats itself in a number of cases, you can smell the existence of a pro ...
... come across peculiarities, make a note of them and just forget about them for the present. You may treat them as curies or freaks just as you do when you see a person with more than five fingers in a hand. If a certain pattern repeats itself in a number of cases, you can smell the existence of a pro ...