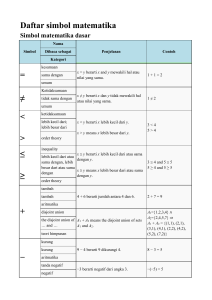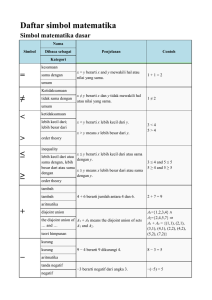
Daftar simbol matematika - Wikipedia bahasa Indonesia
... another name for y (but note that ≡ can also mean other things, such as congruence). ...
... another name for y (but note that ≡ can also mean other things, such as congruence). ...
PA Ch_5 ISG
... We solve rational algebraic equation basically the same way as we solved integers equations, except for one time: when the variable is being multiplied by a _______________. To solve an equation like this: ...
... We solve rational algebraic equation basically the same way as we solved integers equations, except for one time: when the variable is being multiplied by a _______________. To solve an equation like this: ...
Year 2 programme of study
... recall and use multiplication and division facts for the 2, 5 and 10 multiplication tables, including recognising odd and even numbers calculate mathematical statements for multiplication and division within the multiplication tables and write them using the multiplication (×), division (÷) and ...
... recall and use multiplication and division facts for the 2, 5 and 10 multiplication tables, including recognising odd and even numbers calculate mathematical statements for multiplication and division within the multiplication tables and write them using the multiplication (×), division (÷) and ...
Chapter 1 Elementary Number Theory
... which is due to the mathematician Cantor. Numbers are still studied by mathematicians nowadays, in a branch of mathematics called number theory. Numbers have also been of great interest for computer scientists. While it is fairly easy for a computer to represent an integer number (not ”too big”) in ...
... which is due to the mathematician Cantor. Numbers are still studied by mathematicians nowadays, in a branch of mathematics called number theory. Numbers have also been of great interest for computer scientists. While it is fairly easy for a computer to represent an integer number (not ”too big”) in ...
UNIT_10
... Main Teaching Point: Properties of natural numbers Teaching-Learning Process: The teaching of natural numbers can be approached in two ways, either by following the history of the development of number concept, or by simulating the same through activities in the classroom. In both the cases, the key ...
... Main Teaching Point: Properties of natural numbers Teaching-Learning Process: The teaching of natural numbers can be approached in two ways, either by following the history of the development of number concept, or by simulating the same through activities in the classroom. In both the cases, the key ...
Real Numbers and Monotone Sequences
... and obscures the simple algebra. Also, for greater clarity the proof is presented (as are many proofs) backwards from the natural procedure by which it would have been discovered; cf. Question 1.4/1. 3. In the proof that an is bounded by 3, it is easy enough to guess from the form of an that one sho ...
... and obscures the simple algebra. Also, for greater clarity the proof is presented (as are many proofs) backwards from the natural procedure by which it would have been discovered; cf. Question 1.4/1. 3. In the proof that an is bounded by 3, it is easy enough to guess from the form of an that one sho ...
The difficulty of prime factorization is a - Dimes
... The importance of the prime factorization problem is very well known (e.g., many security protocols are based on the impossibility of a fast factorization of integers on traditional computers). It is necessary from a number k to establish two primes a and b giving k = a · b. Usually, k is written in ...
... The importance of the prime factorization problem is very well known (e.g., many security protocols are based on the impossibility of a fast factorization of integers on traditional computers). It is necessary from a number k to establish two primes a and b giving k = a · b. Usually, k is written in ...
Full text
... and n such that mn < 2,000,000 and for other selected values of m and n with mn as large as 167,961,600 by calculating the corresponding values of f as described in Lemma 1. Since large values of m and n tended to give the greatest values for the ratio f^im* n)/mn, and since these are the values tha ...
... and n such that mn < 2,000,000 and for other selected values of m and n with mn as large as 167,961,600 by calculating the corresponding values of f as described in Lemma 1. Since large values of m and n tended to give the greatest values for the ratio f^im* n)/mn, and since these are the values tha ...