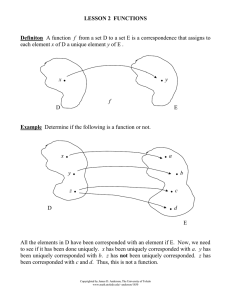
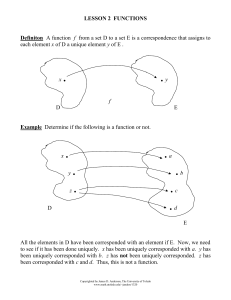
A Pisot number (or P.V. number) is an algebraic integer greater than
... hence 1 is a zero of Q. In [5], we showed that each of Q0 and Q00 has exactly one zero outside D and those two zeros must be real numbers greater than 1. So, if we could find a positive uniform lower bound for β − 1, where β runs over all zeros of Q0 greater than 1, then this would assure that T has ...
... hence 1 is a zero of Q. In [5], we showed that each of Q0 and Q00 has exactly one zero outside D and those two zeros must be real numbers greater than 1. So, if we could find a positive uniform lower bound for β − 1, where β runs over all zeros of Q0 greater than 1, then this would assure that T has ...
Quantum Mechanics and Number Theory
... with residue (−1)k . By choosing the contour as in the figure FIGURE summing up all residues, and taking into account the extra factors exp (βk /2) as well as exp (Eβk ) appearing in the inverse Laplacian transform, we have g (E) = ...
... with residue (−1)k . By choosing the contour as in the figure FIGURE summing up all residues, and taking into account the extra factors exp (βk /2) as well as exp (Eβk ) appearing in the inverse Laplacian transform, we have g (E) = ...
Full text
... From [3], it is known that these polynomials are associated with stacks. Specifically, orthogonal Tchebycheff polynomials are used to calculate the numbers Hkj>n of histories of length n starting at level k and ending at level /, while the reciprocal Tchebycheff polynomials of degree h are used to d ...
... From [3], it is known that these polynomials are associated with stacks. Specifically, orthogonal Tchebycheff polynomials are used to calculate the numbers Hkj>n of histories of length n starting at level k and ending at level /, while the reciprocal Tchebycheff polynomials of degree h are used to d ...
On mathematical induction
... The process we just used to prove that xn = f (n) in the previous section can be formalised as follows. Principle of Mathematical Induction. Suppose that we have a sequence of propositions {Pn }∞ n=0 . (In the previous example the 2n proposition Pn stated that xn = 2 22n+1 . In our course usually a ...
... The process we just used to prove that xn = f (n) in the previous section can be formalised as follows. Principle of Mathematical Induction. Suppose that we have a sequence of propositions {Pn }∞ n=0 . (In the previous example the 2n proposition Pn stated that xn = 2 22n+1 . In our course usually a ...
1 Algebra - Partial Fractions
... Definition 2.1 A sequence is an ordered set of numbers, each being called a term. Example 2.2 2, 5, 10, 17, 26, ..., k 2 + 1, ..., 10001 is a sequence of 100 numbers, the k th term being obtained by squaring k and adding 1. The term k 2 + 1 is known as the general term. Definition 2.3 A series is th ...
... Definition 2.1 A sequence is an ordered set of numbers, each being called a term. Example 2.2 2, 5, 10, 17, 26, ..., k 2 + 1, ..., 10001 is a sequence of 100 numbers, the k th term being obtained by squaring k and adding 1. The term k 2 + 1 is known as the general term. Definition 2.3 A series is th ...
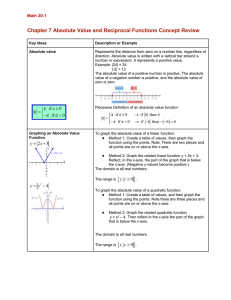
Chapter 7 Absolute Value and Reciprocal Functions Concept Review
... 1. Determine the x-intercepts by setting the expression within the absolute value equal to zero. 2. Use slope (linear function) or direction of opening (quadratic function) to determine which parts of the graph are above or below the xaxis. 3. Keep the parts that are positive (above x-axis) and indi ...
... 1. Determine the x-intercepts by setting the expression within the absolute value equal to zero. 2. Use slope (linear function) or direction of opening (quadratic function) to determine which parts of the graph are above or below the xaxis. 3. Keep the parts that are positive (above x-axis) and indi ...
6-1 Evaluate nth Roots and Use Rational Exponents
... *Operations on Functions: Let f and g be any two functions. A new function h can be defined by performing any of the four basic operations on f and g. Operation Addition ...
... *Operations on Functions: Let f and g be any two functions. A new function h can be defined by performing any of the four basic operations on f and g. Operation Addition ...
PPT
... Suppose f:S → P(S) is a bijection. Let CONFUSEf contain all and only those elements that are not in the sets they map to Since f is onto, exists y S such that f(y) = CONFUSEf. Is y in CONFUSEf ? YES: Definition of CONFUSEf implies no ...
... Suppose f:S → P(S) is a bijection. Let CONFUSEf contain all and only those elements that are not in the sets they map to Since f is onto, exists y S such that f(y) = CONFUSEf. Is y in CONFUSEf ? YES: Definition of CONFUSEf implies no ...
Exam 2 Sol
... (b)(8 pts) We apply the Mean Value Theorem to g(x) on the interval [−b, b] where b is any positive real number. Note that, by assumption, g(x) is (i) continuous on [−b, b], and (ii) differentiable on (−b, b), so the Mean Value Theorem is justified. Now note that since g is odd, we have g(−b) = −g(b) ...
... (b)(8 pts) We apply the Mean Value Theorem to g(x) on the interval [−b, b] where b is any positive real number. Note that, by assumption, g(x) is (i) continuous on [−b, b], and (ii) differentiable on (−b, b), so the Mean Value Theorem is justified. Now note that since g is odd, we have g(−b) = −g(b) ...
Word - The University of Toledo
... Sometimes, the parabola can be sketched using the x-intercept(s) of the quadratic function and/or the axis of symmetry to find the x-coordinate of the vertex of the parabola. If the quadratic function has one x-intercept, then this x-intercept is the vertex of the parabola. To sketch the graph of th ...
... Sometimes, the parabola can be sketched using the x-intercept(s) of the quadratic function and/or the axis of symmetry to find the x-coordinate of the vertex of the parabola. If the quadratic function has one x-intercept, then this x-intercept is the vertex of the parabola. To sketch the graph of th ...