Math Toolkit Practice Packet
... You would expect that men with too small of masses (below 45.4) would make bad marathon runners because their legs would be too short so they would have to pump them too fast. Also men with big masses (over 59.0 kg) would make poor marathon runners because their extra mass would take a lot of extra ...
... You would expect that men with too small of masses (below 45.4) would make bad marathon runners because their legs would be too short so they would have to pump them too fast. Also men with big masses (over 59.0 kg) would make poor marathon runners because their extra mass would take a lot of extra ...
GCF and LCM by Prime Factorization
... GCF helps to efficiently and quickly reduce fractions. One way to determine the GCF is simply by prime factorization. When to use : to reduce fractions Skills needed: multiplication facts, prime factorization Example: 12 & 36 Find the GCF Step 1: Find the Prime factors for 12: 2 x 2 x 3 36: 2 x 2 x ...
... GCF helps to efficiently and quickly reduce fractions. One way to determine the GCF is simply by prime factorization. When to use : to reduce fractions Skills needed: multiplication facts, prime factorization Example: 12 & 36 Find the GCF Step 1: Find the Prime factors for 12: 2 x 2 x 3 36: 2 x 2 x ...
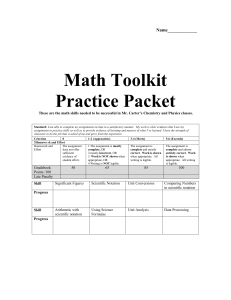
1. Test question here
... 11. The Fibonacci sequence is defined such that the first two numbers in the sequence are both 1 and each successive number is the sum of the two previous numbers in the sequence. The first 5 numbers in the sequence are 1, 1, 2, 3, and 5. What is the greatest common divisor of the 23rd and 24th numb ...
... 11. The Fibonacci sequence is defined such that the first two numbers in the sequence are both 1 and each successive number is the sum of the two previous numbers in the sequence. The first 5 numbers in the sequence are 1, 1, 2, 3, and 5. What is the greatest common divisor of the 23rd and 24th numb ...
Document
... indicates that the integers a and b fall into the same congruence class modulo n = means that integer a is the reminder of the division of integer b by integer n. Example: 14 2 mod 3 and 2 = 14 mod 3 ...
... indicates that the integers a and b fall into the same congruence class modulo n = means that integer a is the reminder of the division of integer b by integer n. Example: 14 2 mod 3 and 2 = 14 mod 3 ...
Troup County School System
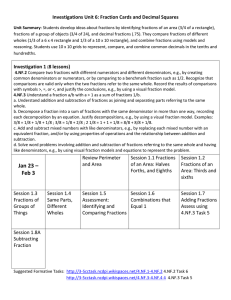
... the product of both denominators. For 1/3 + 1/6, a common denominator is 18, which is the product of 3 and 6. This process should be introduced using visual fraction models to build understanding before moving to the standard algorithm. Students should know that multiplying the denominators will alw ...
... the product of both denominators. For 1/3 + 1/6, a common denominator is 18, which is the product of 3 and 6. This process should be introduced using visual fraction models to build understanding before moving to the standard algorithm. Students should know that multiplying the denominators will alw ...
Arithmetic

Arithmetic or arithmetics (from the Greek ἀριθμός arithmos, ""number"") is the oldest and most elementary branch of mathematics. It consists of the study of numbers, especially the properties of the traditional operations between them—addition, subtraction, multiplication and division. Arithmetic is an elementary part of number theory, and number theory is considered to be one of the top-level divisions of modern mathematics, along with algebra, geometry, and analysis. The terms arithmetic and higher arithmetic were used until the beginning of the 20th century as synonyms for number theory and are sometimes still used to refer to a wider part of number theory.