Calculating Distance in the Complex Plane Lesson
... Step 1) Graph the points and connect them with a line, shown above. The xaxis represents the real numbers and the y-axis represents the imaginary numbers. For example: (2 + 1i) translates to the rectangular coordinates (2, 1) 2 (real number) = x ...
... Step 1) Graph the points and connect them with a line, shown above. The xaxis represents the real numbers and the y-axis represents the imaginary numbers. For example: (2 + 1i) translates to the rectangular coordinates (2, 1) 2 (real number) = x ...
Partners for Student Success - Cecil County Public Schools
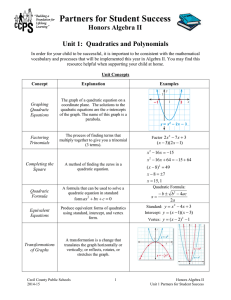
... Honors Algebra II Unit 1: Quadratics and Polynomials In order for your child to be successful, it is important to be consistent with the mathematical vocabulary and processes that will be implemented this year in Algebra II. You may find this resource helpful when supporting your child at home. ...
... Honors Algebra II Unit 1: Quadratics and Polynomials In order for your child to be successful, it is important to be consistent with the mathematical vocabulary and processes that will be implemented this year in Algebra II. You may find this resource helpful when supporting your child at home. ...
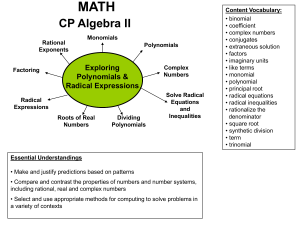
CCGPS Advanced Algebra
... MCC9‐12.A.SSE.2 Use the structure of an expression to identify ways to rewrite it. Use polynomial identities to solve problems. ...
... MCC9‐12.A.SSE.2 Use the structure of an expression to identify ways to rewrite it. Use polynomial identities to solve problems. ...
PreCalculus Fall 2016 Lesson 025 _Fundamental Theorem of Algebra
... Assignment #3: Find the roots (real and imaginary) of the polynomial function and the multiplicities of each root. Medial Summary: A polynomial of degree n has n roots (Fundamental Theorem of Algebra) Roots may be Imaginary Numbers. A polynomial can be factored like: a(x-r1)(x-r2)... where r1, ...
... Assignment #3: Find the roots (real and imaginary) of the polynomial function and the multiplicities of each root. Medial Summary: A polynomial of degree n has n roots (Fundamental Theorem of Algebra) Roots may be Imaginary Numbers. A polynomial can be factored like: a(x-r1)(x-r2)... where r1, ...
polynomial function in x of degree n
... f(x) or less than that number by an even integer 2. The number of negative real zeros of f is wither equal to the number of variations of the sign of f(-x) or less than that number by an even integer ...
... f(x) or less than that number by an even integer 2. The number of negative real zeros of f is wither equal to the number of variations of the sign of f(-x) or less than that number by an even integer ...