7.1 Notes - Issaquah Connect
... Big Idea: You have studied several kinds of nonlinear sequences and functions, which do not have a common difference or a constant slope. In this lesson you will discover that even nonlinear sequences sometimes have a special pattern in their differences. These patterns are often described by polyno ...
... Big Idea: You have studied several kinds of nonlinear sequences and functions, which do not have a common difference or a constant slope. In this lesson you will discover that even nonlinear sequences sometimes have a special pattern in their differences. These patterns are often described by polyno ...
5-1A Use Properties of Exponents
... where an 0 and an is the leading coefficient, n is the degree, and a0 is the constant term. The exponents are all whole numbers. A polynomial function is in standard form if its terms are written in descending order. *Classification of Polynomial functions Example ...
... where an 0 and an is the leading coefficient, n is the degree, and a0 is the constant term. The exponents are all whole numbers. A polynomial function is in standard form if its terms are written in descending order. *Classification of Polynomial functions Example ...
Alternate Proof of Cayley-Hamilton Theorem
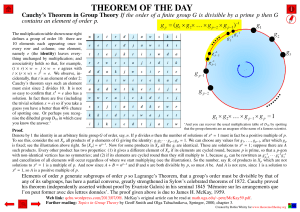
... Proof. Let D(x) be the matrix with polynomial entries D(x)= adj(xI n-A), So D(x)(xI-A)= det(xIn-A)In. Since each entry in D(x) is the determinant of an (n-1) X( (n-1) submatrix of (xIn-A), each entry of D(x) is a polynomial of degree less than or equal to n-1. It folowws that there exist matrices D ...
... Proof. Let D(x) be the matrix with polynomial entries D(x)= adj(xI n-A), So D(x)(xI-A)= det(xIn-A)In. Since each entry in D(x) is the determinant of an (n-1) X( (n-1) submatrix of (xIn-A), each entry of D(x) is a polynomial of degree less than or equal to n-1. It folowws that there exist matrices D ...