Prelim 2 with solutions
... as desired. Finally, it is easy to check that, in cycle notation, σ = (15)(243), a product of two cycles, one of which is odd and the other even. Therefore, σ is odd. (b) (10 points) With σ as in part (a), define τ = (13)σ. Of course, τ is even since σ is odd. Verify that τ (123)(45)τ −1 = (542)(31) ...
... as desired. Finally, it is easy to check that, in cycle notation, σ = (15)(243), a product of two cycles, one of which is odd and the other even. Therefore, σ is odd. (b) (10 points) With σ as in part (a), define τ = (13)σ. Of course, τ is even since σ is odd. Verify that τ (123)(45)τ −1 = (542)(31) ...
Square Roots and Complex Numbers
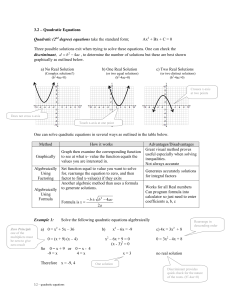
... recognize a perfect square quadratic if a and c are perfect squares. But, whether they are or aren't, a perfect square quadratic must have b= ±2 √ a √ c . Or, if you'd rather look at c, a perfect square quadratic must have c= b 2 /( 4 a ) . ...
... recognize a perfect square quadratic if a and c are perfect squares. But, whether they are or aren't, a perfect square quadratic must have b= ±2 √ a √ c . Or, if you'd rather look at c, a perfect square quadratic must have c= b 2 /( 4 a ) . ...