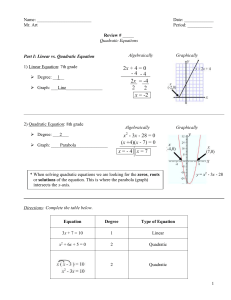
Quadratic Equations - Review - 2012-2013 - Answers
... 1) Standard Form: ax2 + bx + c = 0 (Set equal to zero) x2 term must be positive. Move all terms to the side where + x2 is. If you are given -x2, subtract it over to the other side of the equation to make it positive. ...
... 1) Standard Form: ax2 + bx + c = 0 (Set equal to zero) x2 term must be positive. Move all terms to the side where + x2 is. If you are given -x2, subtract it over to the other side of the equation to make it positive. ...
Turing Machines
... • Two sets have the same cardinality (read: size) if there is a bijective function from one into the other one • The set of the natural numbers is enumerable • The set of all rational numbers are enumerable • Therefore, the set of natural numbers has the same “cardinality” = as the set of rational n ...
... • Two sets have the same cardinality (read: size) if there is a bijective function from one into the other one • The set of the natural numbers is enumerable • The set of all rational numbers are enumerable • Therefore, the set of natural numbers has the same “cardinality” = as the set of rational n ...
12. Polynomials over UFDs
... [12.2] Let k be a field. Show that in the polynomial ring k[x, y] in two variables the ideal I = k[x, y] · x + k[x, y] · y is not principal. Suppose that there were a polynomial P (x, y) such that x = g(x, y) · P (x, y) for some polynomial g and y = h(x, y) · P (x, y) for some polynomial h. An intui ...
... [12.2] Let k be a field. Show that in the polynomial ring k[x, y] in two variables the ideal I = k[x, y] · x + k[x, y] · y is not principal. Suppose that there were a polynomial P (x, y) such that x = g(x, y) · P (x, y) for some polynomial g and y = h(x, y) · P (x, y) for some polynomial h. An intui ...
Complex Numbers and Roots - Bremerton School District
... Solve quadratic equations with complex roots. ...
... Solve quadratic equations with complex roots. ...
CH0 Performance Indicators-Algebra of Calculus Prerequisites
... I can apply the properties of rational exponents to rewrite more complex rational expressions in their simplified equivalent form. ...
... I can apply the properties of rational exponents to rewrite more complex rational expressions in their simplified equivalent form. ...