Module 3 Chapter 5, Irrationals and Iterations pages 55 – 64 Popper
... The Naturals can also be partitioned into {1}, {primes}, and {composites}. Here’s a new partition on the Reals that was discovered in mid nineteenth century: {algebraic numbers} and {transcendental numbers}. The definition of the Transcendental numbers is easy: any real number that is not Algebraic ...
... The Naturals can also be partitioned into {1}, {primes}, and {composites}. Here’s a new partition on the Reals that was discovered in mid nineteenth century: {algebraic numbers} and {transcendental numbers}. The definition of the Transcendental numbers is easy: any real number that is not Algebraic ...
handout - Erickson Math
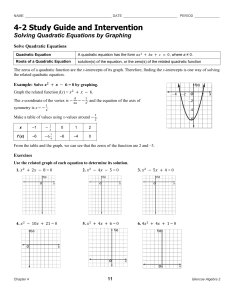
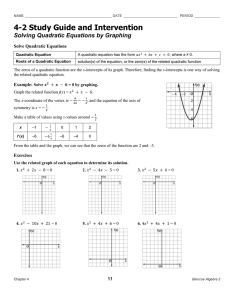
... The zeros of a quadratic function are the x-intercepts of its graph. Therefore, finding the x-intercepts is one way of solving the related quadratic equation. ...
... The zeros of a quadratic function are the x-intercepts of its graph. Therefore, finding the x-intercepts is one way of solving the related quadratic equation. ...
On A Sequence Of Cantor Fractals - Rose
... Since Γ(s) is an intersection of closed subsets of [0, 1], it is a bounded and closed subset of [0, 1], thus by using the Heine-Borel Theorem in R, Γ(s) is compact for every s = 1, 2, · · · . In the first theorem, we obtain an explicit formula for Γ(s). Theorem 1. Let Γ(s) be a Cantor fractal of the ...
... Since Γ(s) is an intersection of closed subsets of [0, 1], it is a bounded and closed subset of [0, 1], thus by using the Heine-Borel Theorem in R, Γ(s) is compact for every s = 1, 2, · · · . In the first theorem, we obtain an explicit formula for Γ(s). Theorem 1. Let Γ(s) be a Cantor fractal of the ...
pythagorean theorem applications2 and outline - Mrs-Cook
... To determine if it is a right triangle, I used the Pythagorean theorem. If the theorem is proven, then the triangle is a right triangle. I plugged the numbers into the theorem (10 had to be c because it is the longest side). I squared the legs and added them together. I compared that the square of t ...
... To determine if it is a right triangle, I used the Pythagorean theorem. If the theorem is proven, then the triangle is a right triangle. I plugged the numbers into the theorem (10 had to be c because it is the longest side). I squared the legs and added them together. I compared that the square of t ...
Math 1
... ab a b when a and b are positive numbers. To multiply radicals: 1. Multiply the outside terms (coefficients) with the outside terms and multiply the inside terms (radicands) with the inside terms. 2. Simplify the resulting radical. Note: In cases where the radicands are large numbers or perfect ...
... ab a b when a and b are positive numbers. To multiply radicals: 1. Multiply the outside terms (coefficients) with the outside terms and multiply the inside terms (radicands) with the inside terms. 2. Simplify the resulting radical. Note: In cases where the radicands are large numbers or perfect ...