II.4. Compactness - Faculty
... Note. Homeomorphic topological spaces are indistinguishable as topological spaces. A set in T1 is open if and only if its image is open in T2 . So homeomorphic topological spaces share all “topological” properties. Example. Let X = (0, 1) and Y = (1, ∞) where T1 is the usual topology on X and T2 is ...
... Note. Homeomorphic topological spaces are indistinguishable as topological spaces. A set in T1 is open if and only if its image is open in T2 . So homeomorphic topological spaces share all “topological” properties. Example. Let X = (0, 1) and Y = (1, ∞) where T1 is the usual topology on X and T2 is ...
Worksheet 17 (4
... Factorable trinomials such as 2x2 - x - 10 will factor into the product of two binomials; 2x2 - x - 10 = (2x - 5)(x + 2), where: 1. The first terms of the two binomials multiply to give 2x2, the first term of the trinomial. (2xx = 2x2) 2. The last terms of the two binomials multiply to give -10, th ...
... Factorable trinomials such as 2x2 - x - 10 will factor into the product of two binomials; 2x2 - x - 10 = (2x - 5)(x + 2), where: 1. The first terms of the two binomials multiply to give 2x2, the first term of the trinomial. (2xx = 2x2) 2. The last terms of the two binomials multiply to give -10, th ...
CALC 1501 LECTURE NOTES 4. SEqUEnCEs Definition 4.1. A
... (2) S2 = N. This set is unbounded, and therefore, the upper bound for this set does not exist. (3) Let S3 = {sin n, n ∈ N} = {sin 1, sin 2, sin 3, . . . }. This set is bounded above by 1, since sin x ≤ 1 for any x. But is there sup S3 ? If n could attain any real value, then since sin( π2 + 2πk) = 1 ...
... (2) S2 = N. This set is unbounded, and therefore, the upper bound for this set does not exist. (3) Let S3 = {sin n, n ∈ N} = {sin 1, sin 2, sin 3, . . . }. This set is bounded above by 1, since sin x ≤ 1 for any x. But is there sup S3 ? If n could attain any real value, then since sin( π2 + 2πk) = 1 ...
algebra - Fountain Math
... result is 2. What is the value of n? (A) 4 (B) 6 (C) 8 (D) 10 (E) 14 2. Christoph has 9 more baseball trading cards than Miguel. The number of cards that they have combined is 45. If c represents the number of cards Miguel has, which equation correctly represents the situation? (A) 2c + 9 = 45 (B) c ...
... result is 2. What is the value of n? (A) 4 (B) 6 (C) 8 (D) 10 (E) 14 2. Christoph has 9 more baseball trading cards than Miguel. The number of cards that they have combined is 45. If c represents the number of cards Miguel has, which equation correctly represents the situation? (A) 2c + 9 = 45 (B) c ...
Powers of rationals modulo 1 and rational base number systems
... there are infinitely many limit points.” (cf. [25] for instance.) With this problem as a background, Mahler asked in [15] whether there exists a non zero real z such that the fractional part of z (3/2)n for n = 0, 1, . . . fall into [0, 1/2[. It is not known whether such a real — called Z-number — do ...
... there are infinitely many limit points.” (cf. [25] for instance.) With this problem as a background, Mahler asked in [15] whether there exists a non zero real z such that the fractional part of z (3/2)n for n = 0, 1, . . . fall into [0, 1/2[. It is not known whether such a real — called Z-number — do ...
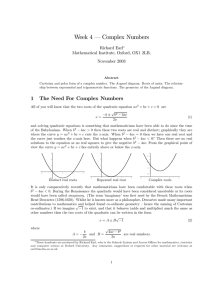
Second Proof: Every Positive Integer is a Frobenius
... It can be shown that N (7, 17, 33) = 61, N (7, 38, 51) = 121 and N (7, 58, 71) = 181. By an application of Lemma 2.6 to the case p = 7, it remains to check the cases when n > 1 and n = 1 mod 420. It can be shown that N (11, 92, 113) = 421 and N (11, 206, 215) = 841. By an application of 2.6 to the c ...
... It can be shown that N (7, 17, 33) = 61, N (7, 38, 51) = 121 and N (7, 58, 71) = 181. By an application of Lemma 2.6 to the case p = 7, it remains to check the cases when n > 1 and n = 1 mod 420. It can be shown that N (11, 92, 113) = 421 and N (11, 206, 215) = 841. By an application of 2.6 to the c ...