Universal Enveloping Algebras (and
... Under bracket multiplication, Lie algebras are non-associative. The idea behind the construction of the universal enveloping algebra of some Lie algebra g is to pass from this non-associative object to its more friendly unital associative counterpart U g (allowing for the use of asociative methods s ...
... Under bracket multiplication, Lie algebras are non-associative. The idea behind the construction of the universal enveloping algebra of some Lie algebra g is to pass from this non-associative object to its more friendly unital associative counterpart U g (allowing for the use of asociative methods s ...
Juliette Hagg
... c. Connections to class work (complex numbers) d. Spreadsheet Activity: Determining the Mandelbrot Set ...
... c. Connections to class work (complex numbers) d. Spreadsheet Activity: Determining the Mandelbrot Set ...
THE DEPTH OF AN IDEAL WITH A GIVEN
... Introduction Let A = K[x1 , . . . , xn ] denote the polynomial ring in n variables over a field K with each deg xi = 1. Let I be a homogeneous ideal of A with I ̸= A and HR the Hilbert function of the quotient algebra R = A/I. Thus HR (q), q = 0, 1, 2, . . ., is the dimension of the subspace of R spa ...
... Introduction Let A = K[x1 , . . . , xn ] denote the polynomial ring in n variables over a field K with each deg xi = 1. Let I be a homogeneous ideal of A with I ̸= A and HR the Hilbert function of the quotient algebra R = A/I. Thus HR (q), q = 0, 1, 2, . . ., is the dimension of the subspace of R spa ...
8. Group algebras and Hecke algebras
... of S. Let R = Q, R, or C. By Proposition 7.16 p∗ : H 1 (S; R) → H 1 (X; R) is injective and maps isomorphically onto H 1 (X; R)H . Therefore, if g ∈ G and ω ∈ H 1 (S; R) then (p∗ )−1 (εH gεH (p∗ ω)) lies in H 1 (S; R). Thus we may realize R[H\G/H] as an algebra of Hecke operators on H 1 (S; R). Line ...
... of S. Let R = Q, R, or C. By Proposition 7.16 p∗ : H 1 (S; R) → H 1 (X; R) is injective and maps isomorphically onto H 1 (X; R)H . Therefore, if g ∈ G and ω ∈ H 1 (S; R) then (p∗ )−1 (εH gεH (p∗ ω)) lies in H 1 (S; R). Thus we may realize R[H\G/H] as an algebra of Hecke operators on H 1 (S; R). Line ...
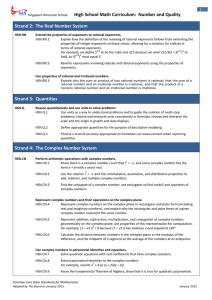
Year 9 Maths Assessment Grid
... angle’. Identify when a circle theorem can be used to help solve a geometrical problem. Understand the use of a graph to represent an inequality in two variables. State the (simple) inequality represented by a shaded region on a graph. Know when to use a dotted/solid line as a boundary for an inequa ...
... angle’. Identify when a circle theorem can be used to help solve a geometrical problem. Understand the use of a graph to represent an inequality in two variables. State the (simple) inequality represented by a shaded region on a graph. Know when to use a dotted/solid line as a boundary for an inequa ...